Rozwiąż nierówność Anonim:

	√3
cos4x<
	2

Proszę mi pomóc bo nie wiem jak rozwiązać ten przykład

Anonim: Byłbym wdzięczny za wskazówkę

Anonim: Płacę gotówką

Mila: Już piszę, gratis

Anonim: @mila bardzo dziękuję 😁

salamandra:

	√3
cos4x<
	2

	√3
cos4x =
	2

cos4x = cos(π/6) 4x = π/6 + 2kπ v 4x = −π/6 + 2kπ / (:4) x = π/24 + 1/2kπ v x = −π/24 + 1/2kπ x∊(π/24 + 1/2kπ ; 11π/24 + 1/2kπ) Powinno być dobrze

Anonim: Dziękuję

Anonim: Ale dlaczego zmieniłaś z < na = ? Bo nie rozumiem dlaczego to się zmienia

salamandra:

	√3
rozwiązałem równanie, dla których cos4x =		, aby ustalić krańce, następnie rysujesz
	2

	√3
wykres cos4x, prostą o równaniu y =		i ta prosta przetnie wykres cosinusa właśnie w
	2

wyliczonych w równaniu punktach, i odczytujesz z wykresu przedział gdzie cosinus jest "poniżej" tej prostej

Mila:

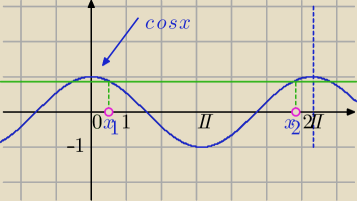
	√3
cos(4x)=		⇔ rozwiązuję w przedziale <0,2π>
	2

	π		11π
4x=		+2kπ lub 4x=		+2kπ
	6		6

	√3
cos(4x)<		⇔
	2

π		11π
	+2kπ<4x<		+2kπ /:4
6		6

π		1		11π		1
	+		kπ<x<		+		kπ
24		2		24		2