trapez
salamandra: Wykaż, że punkt przecięcia się przekątnych trapezu o podstawach a i b, gdzie a>b, dzieli te
przekątne w stosunku a/b. Tego zadania to akurat nie wiem jak zacząć, domyślam się, że jakoś z
podobieństwa, ale co po kolei?
16 gru 21:59
jc: Po narysowaniu przekątnych zobaczysz dwa podobne trójkąty przyklejone do podstaw.
16 gru 22:06
Mila:
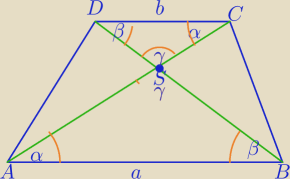
| | a | |
1) ΔABS∼ΔDCS (cecha kkk) w skali k= |
| ⇔ |
| | b | |
?
napisz sam
16 gru 22:06
salamandra: Skąd wiadomo że przy C jest α?
16 gru 22:08
a@b:
O kątach naprzemianległych słyszałeś?

16 gru 22:10
salamandra: Nie

16 gru 22:13
16 gru 22:19
salamandra: I który to byłby przypadek patrząc na te przykłady z linku?
16 gru 22:21
a@b:
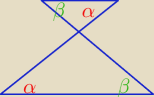
16 gru 22:23
Mila:
Proste równoległe AB i CD przecięte prostą AC
Proste równoległe AB i CD przecięte prostą BD
16 gru 22:27
16 gru 22:29
a@b:
Czytaj ostatni wpis z linku
16 gru 22:32
salamandra:
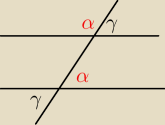
Odwołuję się do przedostatniego przykładu z linku − a α przedstawia naszą sytuację, tak?
16 gru 22:35
Mila:
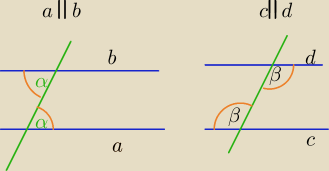
α− kąty naprzemianległe wewnętrzne są równe
β−kąty naprzemianległe wewnętrzne są równe
16 gru 22:45
Mila:
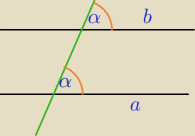
a||b
α− kąty odpowiadające są równe
16 gru 22:48
Mila:
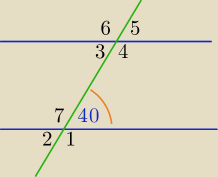
Wypisz miary kątów oznaczonych liczbami od 1 do 7.
16 gru 22:50
salamandra: 1− 140
2− 40
3− 40
4− 140
5− 40
6− 40
7− 140
16 gru 23:02
Mila:
5 i 6 −kąty przyległe to |∡6|=140o,
albo z własności : 4 i 6− katy wierzchołkowe są równe to |∡6|=|∡4|=140o,
16 gru 23:08
salamandra: a 5 i 3 to nie wierzchołkowe?
16 gru 23:12
salamandra: tfu, źle przeczytałem
16 gru 23:12
salamandra: 4 i 6 to wierzchołkowe, stąd też 6 = 140, racja
16 gru 23:13
Mila:
5 i 3 też wierzchołkowe.
Dobranoc

Jutro popracujesz.
16 gru 23:27
salamandra: 5 i 3 tez wierzchołkowe, na początku źle przeczytałem, jakoby chodziło o 3 a nie o 6. Dziękuję,
dobrej nocy

16 gru 23:28




 Odwołuję się do przedostatniego przykładu z linku − a α przedstawia naszą sytuację, tak?
Odwołuję się do przedostatniego przykładu z linku − a α przedstawia naszą sytuację, tak?
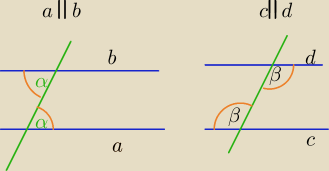 α− kąty naprzemianległe wewnętrzne są równe
β−kąty naprzemianległe wewnętrzne są równe
α− kąty naprzemianległe wewnętrzne są równe
β−kąty naprzemianległe wewnętrzne są równe
 a||b
α− kąty odpowiadające są równe
a||b
α− kąty odpowiadające są równe
 Wypisz miary kątów oznaczonych liczbami od 1 do 7.
Wypisz miary kątów oznaczonych liczbami od 1 do 7.
 Jutro popracujesz.
Jutro popracujesz.
