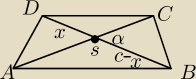
trapezy salamandra: Wykaż, że pole P trapezu równoramiennego o przekątnych długości c i przecinających się pod

	1
kątem α, określone jest wzorem P =		c2*sinα
	2

Policzyłem pola czterech trójkątów, tj: P ABS = 1/2 * (c−x)² * sin(180−α) P BSC = 1/2 * (c−x)² * sin(α) P DSC = 1/2 * x² * sin(180−α) P ASD = 1/2 * x(c−x)*sin(α) I przy dodawaniu tych pól nie wychodzi mi ten wyjściowy wzór.

ICSP: pole P_BSC źle policzone.

salamandra: No tak, racja, dzięki. Ale i tak chyba będę miał dużo liczenia − czy mogę sin(180−α) zamienić na sin(α)? Dużo powinno mi to ułatwić

ICSP: możesz

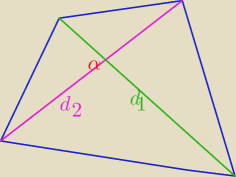
a@b: Pole każdego czworokąta wypukłego jest równe

	1
P=		d1*d2*sinα
	2

to dla tego trapezu

	1		1
P=		*c*c*sinα =		*c2*sinα
	2		2

salamandra:

	1		1
1) P ABS = (		c2−cx+		x2)*sin(180−α)
	2		2

	1		1
2) P BSC = (		c2−cx+		x2)*sin(α)
	2		2

	1		1		1
3) P DSC = (		*(c−x)*x*sin(α) = (		cx−		x2)*sin(α)
	2		2		2

	1		1
4) P ASD = (		cx−		x2)*sin(α)
	2		2

	1		1
1)		c2*sinα − cx*sinα +		x2sinα
	2		2

	1		1
2)		c2*sinα − cxsinα+		x2sinα
	2		2

	1
3)		x2sinα
	2

	1		1
4)		cxsinα −		x2sinα
	2		2

	1		1		1		1
1+2 =		c2*sinα − cx*sinα +		x2sinα +		c2*sinα − cxsinα+		x2sinα =
	2		2		2		2

c²sinα−2cxsinα+x²sinα

	1		1		1		1
3+4 =		x2sinα +		cxsinα −		x2sinα =		cxsinα
	2		2		2		2

No i jak dodam te dwa do siebie to nie wyjdzie mi ten wyjściowy wzór, gdzie popełniłem błąd?

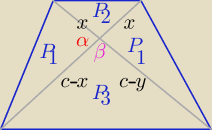
a@b: sinβ= sinα 2P₁=x(c−x)*sinα

	1
P2=		*x2sinα
	2

	1
P3=		(c−x)2sinα
	2

+−−−−−−−−−−−−−−−−−−−−−−−−−−

	sinα
P=		(2cx−2x2+x2−2cx+c2+x2)=...........
	2

a@b: Na rys. po prawej też ma być c−x (sorry

salamandra: Eh, już chyba znalazłem błąd, ICSP powiedział, że pole BSC źle policzone, a ja przekreśliłem pole DSC.

a@b:

salamandra: Mimo wszystko dziękuję za inny sposób, zerknę na pewno, jak rozwiąże swoim

a@b: "szanuj czas" ! ( bo jest on na maturze "droższy od pieniędzy" Nie pisz takich "rozwlekłych" rozwiązań !

salamandra: jak się nie ma innego pomysłu, to czasami tylko takie rozwiązania wchodzą w grę

a@b: Trening .... czyni mistrza

salamandra: Miałem maturę próbną w tamtym tygodniu, być może stówka wpadnie, więc to mnie motywuje do jeszcze większej pracy

a@b: I tak trzymaj !

salamandra: cieszę się, że trafiłem też tu, bo od września dużo się dzięki Wam dowiedziałem i nauczyłem, bo nie sztuką jest spisać gotowe zadanie, ale poznawać nowe sposoby, zasady rozwiązywania zadań

a@b: Na zdrowie

salamandra: Wyszło moim sposobem również

a@b: To taki sam sposób Ty go ..................... rozwlekle zapisałeś

salamandra: Zasugerowałem się wskazówką w książce, która obliczyła pole jednego z trójkątów i zasugerowała dodanie ich wszystkich do siebie

a@b: Zapamiętaj co napisałam we wpisie 21:11

salamandra: Wiem, znam ten wzór, ale tu jednak trzeba było wykazać, to poszedłem tą drogą

a@b: Ok Powodzenia w następnych zadankach

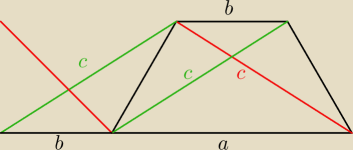
an: Przecież można wykazać właściwie bez liczenia,wystarczą dwie "kreski" równoległe do przekątnych

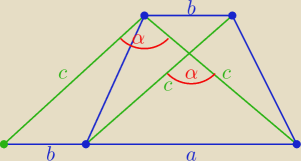
a@b: Jasne, jasne Jeszcze tylko α nie zaznaczyłeś