Relacja równoważności klasa abstrakcji masterchlop: Niech ~ będzie relacją na R² daną wzorem (a,b)~(x,y)<=> a²+b²=x²+y² a) pokaz ze to relacja równoważności; b)Wyznacz[(0,1)]∼ c) Podaj nieskończony zbiór elementów parami nierównoważnych podpunkt A umiem zrobić, ale nie pozostałe tak gdybam sobie z tym b że ta klasa abstrakcji może być równa 2 bo albo x będzie 1 a y 0 bądź na odwrót. Ale nie wiem do końca co to.

PW: b) wszystkie pary wchodzące w relację "∼" z parą (0,1), czyli takie pary (x, y), dla których 0² + 1² = x² + y² x² + y² = 1 (na obrazku pary te tworzą okrąg o środku (0, 0) i promieniu 1).

ite: b/ Ta klasa abstrakcji będzie zbiorem par liczb rzeczywistych, tak wynika ze wzoru, który ja określa. Teraz tylko trzeba poszukać jakich par.

masterchlop: {x,y∊R:x²+y²=1} takie coś?

PW: Dostałęś odpowiedź o 20:55. Jeśli już musisz formalnie zapisać, to {(x, y)∊R²: x²+y²=1} (Twój zapis jest zły − poruszamy się w zbiorze par, więc w odpowiedzi muszą być pary liczb).

masterchlop: Racja, mój błąd a ten podpunkt c)

masterchlop: może potęgi liczb pierwszych w c ?

Adamm: To jest proste, jak wie się cokolwiek o relacjach równoważności. Każdą relację równoważności określa funkcja − i na odwrót. Oczywiście, niekoniecznie taka sama funkcja. Tutaj, f(x, y) = x²+y² jest taką funkcją. Klasy abstrakcji (lub zbiory puste) to po prostu zbiory f⁻¹(a), a∊R

Adamm: a) bo zdefiniowana przez funkcję f b) f(0, 1) = 1, [(0, 1)]_~ = f⁻¹(1) = {(x, y) : x²+y² = 1 } − okrąg c) f⁻¹(x) dla x≥0 to wszystkie klasy abstrakcji wystarczy wybrać po jednym elemencie z każdej

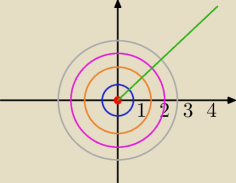
ite: Oto klasy abstrakcji tej relacji (te okręgi) i propozycja sposobu wyboru nieskończonego zbioru elementów parami nierównoważnych.

masterchlop: Dziekuję

Adamm: Eh. Ja wierzę w aksjomat wyboru, po prostu wybieram.

ite: Jestem strzelcem ♐, nie mogłam nie narysować tak pięknej tarczy.