tabela zmienności funkcji kruciutko: Hej, mam zbadać zmienność funkcji f(x)= (x+1)/(x−1). Mam problem z tabelą, otóż wyszło mi że pierwsza jak i druga pochodna nie mają miejsc zerowych. Jak w takim razie powinna wyglądać tabelka?

ite: A jaka jest dziedzina tej funkcji ? To od niej będzie zależeć tabela.

kruciutko: zbiór liczb rzeczywistych bez 1

ite: To trzeba jeszcze sprawdzić, dla jakich argumentów pierwsza pochodna przyjmuje wartości dodatnie i ujemne, a dla jakich druga.

kruciutko: to też mam, (−oo,1) pierwsza i druga ujemne (1,+oo) pierwsza ujemna druga dodatnie

ite: W takim razie tabela będzie mieć dwie kolumny dla argumentów z przedziału (−∞,1) i dla (1,+∞). x | (−∞,1) | (1,+∞) | f(x) f'(x) f''(x)

kruciutko: i co moge powiedziec z tej tabeli o f(x)?

ite: Najpierw musisz ją uzupełnić informacjami, które podałeś 20:07.

a@b:

	2
f(x)=		+1 , x≠0
	x−1

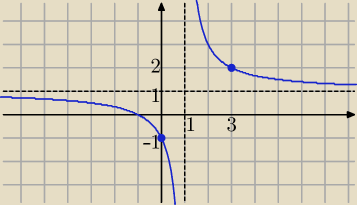
wykresem hiperbola wyżej Funkcja rosnąca w całej dziedzinie ( nie ma ekstremum asymptoty : pionowa x= 1 i pozioma y= 1 miejsce zerowe x_o= −1

kruciutko: x | (−∞,1) | (1,+∞) | f(x) ? ? f'(x) − − f''(x) − + i co w tych znakach zapytania?

a@b: króciutko

ite: Pierwsza pochodna przyjmująca wartości ujemne oznacza, że funkcja jest malejąca czyli ↘ | ↘ w obu rubrykach. W tym przedziale, w którym druga pochodna jest ujemna, funkcja jest wklęsła. W tym drugim przedziale, w którym druga pochodna jest dodatnia, funkcja jest wypukła. Ta informacja pomaga narysować wykres, ale tu juź masz narysowany : ).

ite: i to narysowany szybciutko

kruciutko: krucuitko to pseudonim matematyczny Dziękuje za pomoc rysunek jak najbardziej się przyda, natomiast zależało mi najbardziej na tym opisie z 20:34