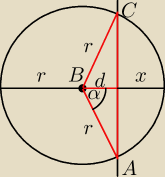
Okrąg, pole Szkolniak: Okrągła pizza o średnicy 32 została przecięta wzdłuż prostej, która jest odległa od środka pizzy o 8. Wyznacz pole mniejszego kawałka pizzy. r=16 d=8 ⇒ x=d=8

	d		1
cosα=		=		⇒ α=60°
	r		2

P_w − pole wycinka koła

	2α		1		256
Pw=		*πr2=		*256π=		π
	360°		3		3

P_Δ − pole trójkąta ABC

	1		256		√3
PΔ=		*r2*sin120°=		*		=64√3
	2		2		2

P − pole mniejszego kawałka

	256
P=Pw−PΔ=		π−64√3
	3

Dobrze rozwiązane?

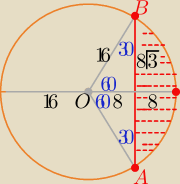a@b: Nie marnuj czasu na takie długie rozpisywanie ΔAOB =2 trójkąty "ekierkowe" o kątach ostrych 30^o,60^o |∡AOB|=120^o

	1
P=Pw−P(ΔAOB) i krótko : P(ΔAOB)=8*8√3=64√3 , Pw=		Pk
	3

	64
P=		(4π−√3)
	3

a@b: Poprawiam chochlika

	64
P=		(4π−3√3)
	3

Szkolniak: Dzięki piękne a@b

a@b: Na zdrowie