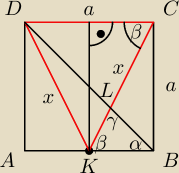
Kwadrat, tangens Szkolniak: W kwadracie ABCD punkt K jest środkiem boku AB. Odcinki BD i KC przecinają się w punkcie L. Wyznacz tangensy kątów trójkąta KBL. a − bok kwadratu przekątna kwadratu podzieliła kąt prosty przy wierzchołku B na dwa równe kąty po 45 stopni, z tego wynika, że tgα=tg45°=1 x=|CK|=|DK| wyznaczamy x z twierdzenia Pitagorasa:

	1		√5
x2=a2+		a2 ⇒ x=		a
	4		2

wykorzystujemy teraz dwa wzory na pole ΔCDK i porównujemy ich prawe strony:

	a2
P=
	2

	1		a		√5a		sinβ*a2√5
P=2*		*		*		*sinβ=
	2		2		2		4

	sinβ*a2√5		a2
		=		/*4
	4		2

	2√5
sinβ*a2√5=2a2 ⇒ sinβ=
	5

	a		2		√5
cosβ=		*		=
	2		√5a		5

	sinβ
tgβ=		=2
	cosβ

w tym momencie mam wyznaczone tangensy dwóch kątów, natomiast jak wyznaczyć tangens kąta gamma?

a7:

	CB
tgβ=		=2
	KB

Szkolniak: Z Warszawy do Katowic przez Gdańsk z tym tgβ co do tgγ jakiś pomysł?

a7: ΔDCL jest podobny do ΔKBL w skali 2 (gdyz podstawy są w skali 2: a do a/2) i teraz mamy wszytskie boki obu trójkątów gdyż łatwo je wyliczyć i liczymy sinγ z tw. sinusów, cosγ z tw. cosinusów i mamy tgγ może jest prostszy sposób, ale ten jest ok

	a√5		a		a√2
KL=		KB=		LB=
	6		2		3

jc:

	tg α + tg β		1+2
tg γ = tg(180 − α − β) = − tg(α+β)=−		= −		=3
	1− tg α tg β		1−1*2

a7:

	6√5		13√10
wychodzi mi sinγ=		cosγ=
	6		40

tgγ24√2

Szkolniak: Super, dzięki za pomoc

a7: o jest prostszy sposób

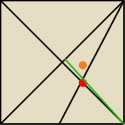
jc: Czerwona kropka odcina 1/3 zielonego odcinka (to punkt przecięcia środkowych). Dlatego tg (pomarańczowa kropka) = 3.

jc: a7, o czymś takom myślałeś, czy o czymś jeszcze prostszym?

a7: jc ja nie rozumiem tego sposobu ze środkowymi ( wiem, że przecinają się w 1/3 ) ale co mają do tangensa, bo tego nie rozumiem, coś nie kumam

a7: nie, myślałam właśnie raczej o takim jak napisałeś 20:09

jc: tg = (od środka kwadratu do wierzchołka kwadratu)/(od środka do czerwonej kropki) = 3 Sam napisałeś , że kąt γ mamy też po drugiej stronie − powyżej pomarańczowa kropka.

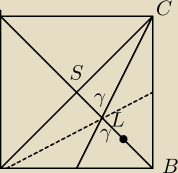
jc: tg γ = CS / LS = 3 bo LS = 1/3 BS = 1/3 CS

a7: jasne, teraz widzę i rozumiem , dzięki

a7: tak tak już załapałam