z góry bardzo dziękuję, chodzi o sam sposób rozwiązania jakzdacmature: Witam. Czy mógłby ktoś wytłumaczyć mi postępowanie przy robieniu tego typu zadań? Wyznacz wartości (o ile istnieją) funkcji f: największą (M) i najmniejszą (m) w podanym zbiorze: a) f(x)= x² / (4 + x) ; x ∊ < −10, −5 > ∪ < −3, 5 > c) f(x)= 10x / (x² +1) ; x ∊ (0,10) d) f(x)= 1/ (x² −4) ; x ∊ <1,2) ∪ (2,3>

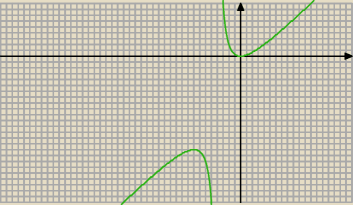
a7: 1.wyznaczamy dziedzinę 2.liczymy pierwszą pochodną i sprawdzamy kiedy jest ona równa zero 3.liczymy wartości na krańcach zbioru i na iksach, gdzie zeruje się pochodna 4. pomocniczo możemy wykonać rysunek poglądowy nie wiem czy potrzebne jest liczenie drugiej pochodnej a) U{x²}{4+x) x∊R\{−4} jest asymptota pionowa

	2(4+x)−x2
f'(x)=		=.....
	(4+x)2

	100		9		25
f(−10)=		f(5)=−25 f(−3)=		f(5)=
	14		7		9

	25
odp. wartość najmniejsza w podanym zbiorze dla podanej funkcji to −25, a największa
	9

jakzdacmature: dziękuję bardzo! mała poprawka w przykładzie a) mianownik pochodnej wynosi x² + 8x+ x(x+8) pochodna zatem zeruje się w x0=0 i x0= −8 z obliczeń wychodzi, że f(−3)= 9 i f(−10)= −50/3 i to się zgadza natomiast zgodnie z odpowiedziami w przypadku c) wartość najmniejsza nie istnieje, a w przypadku d) nie istnieje wartości najmniejsza, ani wartość największa jak do tego dojść?

jakzdacmature: ah, co ja bredzę *licznik

ICSP:

	x2		16
f(x) =		= (x−4) +
	x + 4		x + 4

	16
f' = 1 −		= 0 ⇒ x = 0 v x = −8
	(x+4)2

jakzdacmature: dziękuję! a jak to wygląda w przypadku d) i c)?

ICSP: (x − 1)² ≥ 0 x² + 1 ≥ 2x

2x
	≤ 1
x2 + 1

10x
	≤ 5
x2 + 1

f(x) ≤ 5 widać kiedy zajdzie równość. Maksimum zatem istnieje i jest równe 5. Minimum oczekiwać nie możemy gdyż funkcja rośnie (0 ; 1) osiąga maksimum a następnie maleje. Gdyby rozważany zbiór byłby domknięty to minimum byłoby równe jednej z wartości f(0) , f(10)

ICSP: Wszystko praktycznie da się odczytać z monotoniczności i z dobrego rysunku.

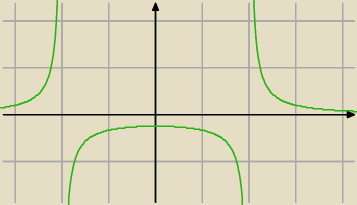
a7: funkcja ma dwie asymptoty 2 i −2 i na podanych przedziałach przy dwójce z lewej strony dąży do −∞, a przy dwójce z prawej strony dąży do +∞ dla 1 i 3 jesteśmy w stanie policzyć wartości dla x→2 trzeba policzyć granice z prawej i lewej strony

jakzdacmature: jak rozwiązanie wyglądałoby z wykorzystaniem pochodnej funkcji?

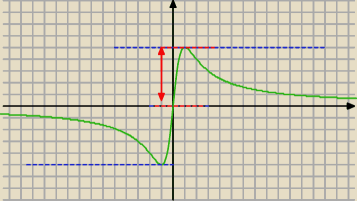
a7: c) najmniejsza wartość na przedziale <0,10> to 0 dla x=0 a największa to 5 dla x=1

a7: no to policz pochodną c) i d) i jej miejsca zerowe ok?

a7: c) poprawka tutaj masz zbiór bez domknięć, więc nie da się określić najmniejszej i największej wartości ale haczyk

jakzdacmature: w c) rozpatrujemy przedział otwarty (0, 10) i zgodnie z odpowiedziami najmniejsza wartość nie istnieje w przykładzie d) f(1) = −1/3 f(3) = 1/5 granica lewostronna dla 2 wynosi +∞ granica prawostronna dla 2 wynosi −∞ co z tym zrobić dalej?..

jakzdacmature: no właśnie, dlaczego nie da się określić tych wartości?

a7: najmniejsza wartość jakby dąży do zera ale to nie zero, największa to 5 dla x=1

jakzdacmature: dla c) wartość max wynosi 5, nie istnieje jedynie wartość min

a7: jak masz przedział otwarty to masz super małą liczbę, ale jej nie dasz rady określić, bo zawsze istnieje super mała liczba od niej o ciutkę mniejsza− tak się myśli−podchodzi w matematyce

a7: 00:57 tak (rozumiem, że pochodna ma miejsce zerowe w x=1 bo tak to wygląda na rysunku)

jakzdacmature: a w jaki sposób zobrazować to na obliczeniach?

a7: 00:55 obliczyłeś i wyciągasz wnioski, które krótko opisujesz jeśli y dązy do ±∞ to nie ma granicy liczbowej

a7: to może zacznijmy przykład d) od początku liczysz asymptoty i to jest łatwe liczysz pochodną i skoro jest miejsce zerowe to znaczy że zmieniła się z rosnącej na malejącą lub odwrotnie z malejącej na rosnącą teraz sprawdzasz dla kilku punktów jak to jest w tym przedziale, potem liczysz te granice przy asymptocie x=2 i masz odpowiedź że przy x=2 funkcja nie ma granic liczbowych a w jedynce ma wartość(najmniejszą dla podanego zbioru) −1/3 w x=3 1/3 robisz rysunek poglądowy i to chyba wszystko? wolałabym żeby jeszcze ktoś zweryfikował to, co napisałam

a7: sprostowanie −1/3 nie jest wartością najmniejszą skoro dla x=2 jest −∞

jakzdacmature: przykład c) jest już dla mnie jasny, ale d) nadal pozostaje zagadką nie do rozwikłania dla 2 nie ma wartości min i max, ale przecież 2 nie jest w naszym przedziale, nie należy do dziedziny dlaczego więc wartośc min i max nie istnieją?

jakzdacmature: dobra, chyba rozumiem 2 nie należy do zbioru, który rozpatrujemy, ale przykładowo 1,999999 i 2,000001 już tak dla x= 1,999999 y= −250 000 dla x= 2,000001 y= 250 000 i te wartości w miarę zbliżania się do 2 będą odpowiednio− maleć i rosnąć, więc wartość max i min nie istnieją dobrze myślę?

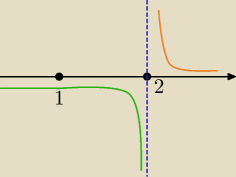
a7: masz tam przedziały otwarte przy dwójce czyli właśnie okazuje się, że tam będzie ±∞ (z lewej strony −∞, z prawej strony +∞) czyli dla sumy tych przedziałów nie ma wartości największej ani najmniejszej napisz proszę czego nie rozumiesz zaczynając od początku w razie czego i ja spróbuję wychwycić, gdzie jest problem

a7: 1:33 właśnie o to chodzi

jakzdacmature: no i bingo dziękuję, wspólnymi siłami dałyśmy radę niedługo wrócę tu z geometrią analityczną, ugh...

a7: