grafy mat123: Udowodnij, że dowolny graf rzędu 6 zawiera K3 lub K3⁻ jako graf indukowany. Robię to tak, że wybieram jeden wierzchołek i teraz mam 2 przypadki. Albo istnieje taka 3 pozostałych wierzchołków, które sąsiadują z moim wybranym wierzchołkiem. Lub przypadek drugi, kiedy nie istnieje taka trójka. Dla 1−ego przypadku pewne dwa z trzech sąsiadują z moim wybranym wierzchołkiem i tworzą graf pełny. Natomiast co będzie w 2−gim przypadku? Wychodzi na to, że żadne z nich nie sąsiadują? I jeżeli tak to co w związku z tym?

Pytający: Zacznij od poprawnego rozpatrzenia pierwszego przypadku. Masz w nim przecież zapewnione, że "istnieje taka 3 pozostałych wierzchołków, które sąsiadują z moim wybranym wierzchołkiem", zatem oczywistym jest, że "pewne dwa z trzech sąsiadują z moim wybranym wierzchołkiem" (a nawet każde 2 z tych 3), jednak nie wiadomo skąd wniosek, że "tworzą graf pełny".

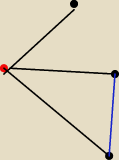
mat123: Czyli moja sytuacja wygląda tak.(Wybrany wierzchołek jest czerwony) I teraz muszę udowodnić że istnieje ta niebieska krawędź?

mat123: No to jeżeli taka krawędź nie istnieje => dla pozostałych 2 wierzchołków z 1 z wierzchołka z "wybranych" istnieje K3⁻ W przeciwnym przypadku, gdy niebieska krawędź istnieje => istnieje K3 Coś takiego?

Pytający: Tak, coś na tej zasadzie. Jeśli istnieje krawędź pomiędzy dowolnymi 2 z tych 3 sąsiadujących z wybranym, to te 2 i ten wybrany tworzą K₃. Jeśli taka krawędź nie istnieje, to te 3 wierzchołki sąsiadujące tworzą dopełnienie K₃.

Pytający: A w drugim przypadku istnieją 3 wierzchołki niesąsiadujące z wybranym i reszta rozumowania jest analogiczna do pierwszego przypadku (tylko na odwrót).

mat123: Dziękuję za pomoc

mat123: Zastanawiam się tak teraz, czy rząd tego grafu ma jakieś znaczenie czy zachodzi to również dla grafu rzędu 4? Bo tak naprawdę to nie wykorzystujemy pozostałych dwóch wierzchołków

mat123: Chodzi mi o to, że nie widzę momentu, gdzie była zastosowana tutaj zasada szufladkowania.

Pytający: Masz 6 wierzchołków, więc poza wybranym wierzchołkiem jest 5 pozostałych wierzchołków. Wśród nich każdy sąsiaduje z wybranym lub nie (znaczy masz 5 elementów należących 2 zbiorów). Zatem musi istnieć zbiór mający co najmniej 3 elementy (znaczy musi zachodzić pierwszy lub drugi przypadek podany wyżej). Dla grafu rzędu 4 nie ma takiej pewności, przykład na rysunku. I zasada szufladkowa, nie szufladkowania.

mat123: Teraz rozumiem i dziękuję za pomoc oraz za poprawienie

mat123: A czy w drugim przypadku w obu "podprzypadkach" nie powstaje dopełnienie K₃. Nie powstaje wcale K₃?

.: po prostu dopełnienie K3 to graf pusty więc jeśli nie ma induk. K₃ to na pewno będzie K₃⁻