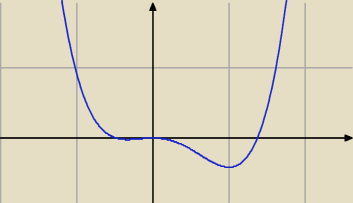
Wyznacz zbiór wartości funkcji. Kuba1347: Wyznacz zbiór wartości funkcji f(x) = ³₄ x⁴ − ²₃ x³ − ¹₂ x² , jeśli x∊<0, 2>. Proszę o wytłumaczenie krok po kroku.

Jerzy: Liczysz f(0) , f(4) i sprawdzasz, czy funkcja posiada ekstremum lokalne w tym przedziale. Jeeśli tak,to obliczasz i ustalasz maksymalny przedział.

Jerzy: Upss ... f(2) oczywiście.

janek191:

	3		2		1
f(x) = x2 *(		x2 −		x −		)
	4		3		2

f'(x) = 3 x³ − 2 x² − x = x*( 3 x² − 2 x − 1) = 0 ⇔ x = 0 lub 3 x² −2 x − 1 = 0 Δ = 4 − 4* 3*(−1) = 16 √Δ = 4

	2 − 4		1
x =		= −		lub x = 1
	6		3

f ''(x) = 9 x² − 4 x − 1 f ''(0) = − 1 f ma w x= 0 maksimum lokalne

	1
f ''( −		) > 0 f ma w x = −U{1}[3} minimum lokalne
	3

f ''( 1) = 9 − 4 − 1 > 0 f ma w x = 1 minimum lokalne

	3		1		5
f(1) =		− U{2}[3} −		= −		< f ( −U{1}{3])
	4		2		12

zaten

	5
ZWf = < −		, + ∞)
	12

a7:

janek191: Pominąłem ,że x ∊ < 0 , 2 >

a7:

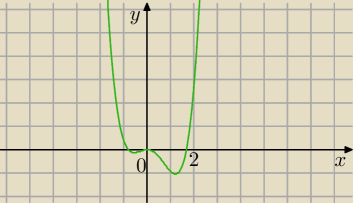
	2
f(0)=0 f(2)=3/4*16−2/3*8−1/2*4=4
	3

Kuba1347: Okej, jeszcze nie czytając waszych odpowiedzi zrobiłem to tak: 1. Obliczyłem pochodną: f'(x) = 3x³ − 2x² − x 3x³ − 2x² − x = ( x² − x )( 3x+1 ) = x( x − 1)( 3x+1 ) x₁ = 0 x₂ = 1 x₃ = − ¹₃ < to jest sprzeczne czyli odpada z przedziału? Proszę o potwierdzenie! 2. Wiem, że teraz trzeba obliczyć ekstrema lokalne, mógłby mi ktoś wyjaśnić dlaczego w x=0, linia odbija się z powrotem w dół? 3. Obliczyłem y dla x₁ = 0 i x₂ = 1 bo x₃ = − ¹₃ odpada bo się nie mieści w przedziale. f(0)=0 f(1)= − ⁵₁₂ 4. Zbiór wartości funkcji to <0, − ⁵₁₂ ? Proszę o potwierdzenie

Kuba1347: No i czy muszę liczyć granicę do +∞ i −∞ jak się zachowuje x poza przedziałami? Jak rysować te ekstrema?

Kuba1347: Dobra, już ogarnąłem jak rysować te ekstrema, powiedzcie tylko czy dobry jest wynik zbiór wartości funkcji to x ∊ <0, − ⁵₁₂ > i czy mam liczyć granice do +∞ i −∞ czy je liczyć tylko jak dziedzina to x należy do wszystkich liczb rzeczywistych?

a7: wartości to y (ygreki)

	5		2
dla x <0,2> y ∊ <−		, 4		>
	12		3

chociaż u mnie na rysunku 17:35 coś się nie zgadza

Kuba1347: Okej, a jeszcze jedno. Y wyznaczam podstawiając X do f(x), nie f'(x)?

Ling Xi :

a7: dla x =1 jest minimum ale funkcji wyjściowej dlatego podstawiamy do f(x)