Całka podwójna
kasia: Oblicz powierzchnię bryły ograniczonej powierzchniami:
x2+y2=9, z=1−x, z=5
Wydaje mi się, że ta bryła będzie nieograniczona. Płaszczyzna z=1−x przetnie walec po skosie,
ale nie będzie on ograniczony od góry i dołu.
Jednak w odp. wynik jest liczbą skończoną (36pi).
Proszę o jakąś wskazówkę.
13 gru 22:40
kasia: Od góry będzie (z=5).
Ale od dołu wciąż nie jest.
13 gru 22:44
jc: Pomijając fakt, że irytuje mnie sformułowanie (bryła ograniczona powierzchniami − jak to
zdefiniować?), to rachunek jest oczywisty. 4*3*3*π=36π.
Patrzymy jak bardzo oddalone są środki elips po obu stronach walca
i mnożymy przez pole przekroju. Należy się jeszcze upewnić, czy denka się nie przecinają.
13 gru 22:47
kasia: Ja próbuję to rysować i kurcze no, nie widzę ograniczenia. Ten walec ucieka mi w
nieskończoność.
Możesz wyjaśnić mi o jakich elipsach mówisz?
13 gru 23:00
kasia: A raczej w minus ∞
13 gru 23:01
Saizou : Skorzystaj z geogebra w 3d i wyrysuj to sobie, to zobaczysz

13 gru 23:03
jc:
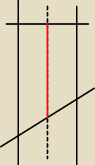
Jak przetniesz pionowy walec poziomą płaszczyzną, to przekrój będzie kołem,
jak skośną, to elipsą. Koło to też elipsa.
13 gru 23:04
kasia: Ubzdurałam sobie, że z=1−x musi ograniczać walec i z góry, i z dołu...

13 gru 23:12
a7:
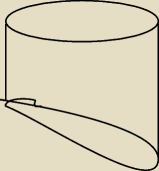
(rysunek poglądowy) wychodzi ścięty walec o promieniu podstawy (górnej) 3
13 gru 23:13
kasia: Dziękuję za pomoc

13 gru 23:14
kasia: Jeszcze mam jedno pytanie. Gdybym chciała to rozbić na sumę całek to byłoby to:
∫∫[K(0,0),3)] 5 dxdy − ∫∫[D] (1−x) dxdy
Gdzie D byłoby można opisać: ∫[1,3]dx ∫[−√9−x2, √9−x2] dy?
13 gru 23:23
kasia: I musi być minus, a nie plus, bo przy tamtej drugiej całce, z−ty są ujemne. Zgadza się? A
docelowo całka liczy nam objętość pod funkcja na danym obszarze. Tak?

13 gru 23:55
kasia: ?

14 gru 11:26
jc: Całkujesz odległość pomiędzy podłogą a sufitem (wykresem funkcji leżącym niżej, wyżej).
Taka odległość to różnica poziomów = wyższy − niższy.
Znaki nie mają znaczenia.
Mówi się, że całka to objętość pod wykresem funkcji. To pewne uproszczenie,
ale tak łatwiej opowiadać. Jak wykres leży poniżej poziomu zero, to już tak prosto
nie jest. Formalnie całka to granica sumy iloczynów zΔxΔz.
Dla z>0 to faktycznie objętość, ale dla z<0 to objętość z minusem.
14 gru 12:13
kasia: Okej, bardzo Ci dziękuję

Mógłbyś jeszcze zerknąć na komentarz z wczoraj 23:23?
14 gru 14:09

 Jak przetniesz pionowy walec poziomą płaszczyzną, to przekrój będzie kołem,
jak skośną, to elipsą. Koło to też elipsa.
Jak przetniesz pionowy walec poziomą płaszczyzną, to przekrój będzie kołem,
jak skośną, to elipsą. Koło to też elipsa.

 (rysunek poglądowy) wychodzi ścięty walec o promieniu podstawy (górnej) 3
(rysunek poglądowy) wychodzi ścięty walec o promieniu podstawy (górnej) 3



 Mógłbyś jeszcze zerknąć na komentarz z wczoraj 23:23?
Mógłbyś jeszcze zerknąć na komentarz z wczoraj 23:23?