Dwa zadania, jedno na dowodzenie a drugie z równaniem z wartością bezwzględną. Konrad: Witam, dzisiaj miałem sprawdzian z matematyki (1 liceum) i nie wiedziałem tylko jak rozwiązać dwa zadania prosiłbym o jakąś małą podpowiedź jak je zrobić. Zad.1 Wykaż że liczba √41−24√2−√41+24√2 jest liczbą niewymierną. Domyślam się, że trzeba wykorzystać wzór √a²=|a|

Konrad: Zad.2 Ile jest rozwiązań równania |x+3|+|2x+6|=p dla zmiennego parametru p. Doszedłem do 3|x+2|=p jednak nie wiem co dalej.

gosc: √(3−4√2)² − √(3+4√2)² = 4√2 −3 − 3 − 4√2 = −6

gosc:

	−6
wychodzi mi ze jest wymierna bo		−6 to calkowita a 1 naturalna
	1

gosc: jedyna trudnosc to rozlozyc 12√2 na 2 liczby i sprawdzac kiedy suma ich kwadratow da 41

gosc: na iloczyn dwoch liczb jak cos

Konrad: Okej, dzięki.

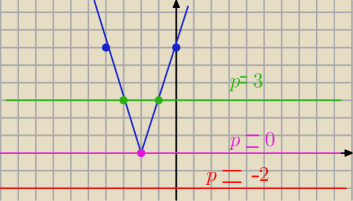
janek191: 3 *I x + 2 I = p Patrz rysunek Powinno być: 3*I x + 3 I = p

PW: Zadanie 1. Niech a = √41−24√2, b = √41+24√2. Ponieważ ab = √41² − (24√2)² = √41² −24²2 = √1681 − 1152 = √529 = 23, widzimy że (a − b)² = a² − 2ab + b² = 41 − 24√2 − 2•23 + 41 + 24√2 = 82 − 46 = 36, zaterm a − b = − 6 jest liczbą wymierną wbrew tezie postawionej w poleceniu. Nie chce mi się wierzyć, że tak sformułowane zadanie kazano rozwiązać uczniom pierwszej klasy na sprawdzianie. Szkoła o wyjątkowych ambicjach?

Saizou : N[PW]] pewnie kolega źle przepisał i miało być wymierną