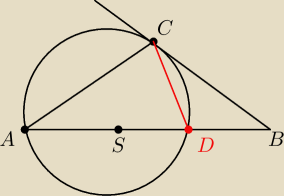
planimetria salamandra: Nie pamiętam słowo w słowo treści zadania, nie mogę go też znaleźć, może wy pomożecie. Dany jest okrąg, styczny w punkcie C do prostej. Wiadomo, że odcinek AC = r√3 i S jest środkiem okręgu. Wykaż, że miara kąta ACB to 120 stopni Ja zrobiłem tak, że dorysowałem cięciwą CD, zauważyłem, że kąt ACD jest kątem prostym, jako kąt oparty na łuku AD (oparty na średnicy) AD = 2r, i CD = r więc zauważam, że to trójkąt 30 60 90, gdzie CAD = 30, CDA = 60, kąt DCB to kąt między styczną a cięciwą. Kąt między styczną a cięciwą CD ma taką samą miarę jak kąt oparty na tej cięciwie, czyli 30 stopni. ACB = 90+30 = 120 c.n.u Zad 2.

	1−x
Wykaż, że dla dowolnej liczby dodatniej x prawdziwa jest nierówność x+		≥1
	x

Mnożę przez x obustronnie, ponieważ x>0, więc przekształcenie będzie równoważne x²+1−x≥x x²−x−x+1≥0 x²−2x+1≥0 (x−1)²≥0 (x−1)²=0 x0 = 1 Rysuję parabolę ramionami do góry, z jednym miejscem zerowym "1" i piszę adnotację, że dla każdego x∊R nierówność jest spełniona. Czy te zadania są dobrze uzasadnione?

a7: zad. 2 gdy masz (x−1)²≥0 to piszesz coś w rodzaju, że Każda liczba rzeczywista podniesiona do kwadratu będzie większa równa zero, więc nierówność jest spełniona dla każdego x>0 zad.1 skąd wywnioskowałeś że |CD|=r musisz to uzasadnić

salamandra: CD = r z właściwości trojkata 30,60,90.

Saizou : U ciebie jest trochę inne rozumowanie zapisanie Chcesz z długości boków wnioskować miary kątów a teraz piszesz że z kątów wnioskujesz długość boku (lepiej pokazać że |CD|=r z tw. Pitagorasa )

salamandra: Wiedziałem ze trojkat o katach 30,60,90 ma boki a, a√3, 2a, i jakoś wyszło, miałem to dziś na maturze próbnej