Prawdopodobiestwo
noname: Ze zbioru cyfr {1,3,4,5,6,7,9} wybieramy trzy razy kolejno po jednej cyfrze bez zwracania i
tworzymy z nich liczbę trzycyfrową rozpoczynając od cyfry stek. Oblicz prawdopodobieństwo, że
uzyskana w ten sposób liczba będzie parzysta.
11 gru 19:30
a7: | | 5 | | 4 | | 2 | | 200 | | 50 | |
P(A)= |
| *5* |
| * |
| = |
| = |
| |
| | 7 | | 6 | | 6 | | 252 | | 63 | |
11 gru 19:46
a7:
| | 5 | | 4 | | 2 | | 40 | | 20 | |
P(A)= |
| *5* |
| 8 |
| = |
| = |
| |
| | 7 | | 6 | | 5 | | 42 | | 21 | |
11 gru 19:55
a7: zamiast "8" powinno być "*" (znak mnożenia)
11 gru 19:56
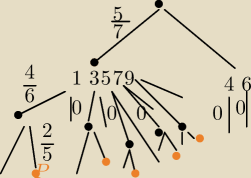
a7: 134 136 146 164 154 164 174 176 194 196
314 316 346 354 356 364 374 376 394 396
514 516 534 536 546 564 574 576 594 596
714 716 734 736 746 764 754 756 794 796
914 916 934 936 946 964 954 956 974 976
416 436 456 476 496
614 634 654 674 694
Ω=9*8*7=504
|A|=10*5+10=60
11 gru 20:16
noname: odpowiedź to 27 ehh
11 gru 20:26
Mila:
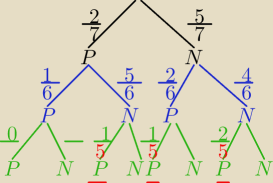
A− utworzono liczbę parzystą
| | 2 | | 5 | | 1 | | 5 | | 2 | | 1 | | 5 | | 4 | | 2 | |
P(A)= |
| * |
| * |
| + |
| * |
| * |
| + |
| * |
| * |
| |
| | 7 | | 6 | | 5 | | 7 | | 6 | | 5 | | 7 | | 6 | | 5 | |
| | 10+10+40 | | 60 | | 2 | |
P(A)= |
| = |
| = |
| |
| | 7*6*5 | | 7*6*5 | | 7 | |
11 gru 20:42
a7: a no tak 20:16 Ω powinna być Ω=7*6*5=210
|A|=60
| | 60 | | 2 | |
czyli P(A)= |
| = |
| echh |
| | 210 | | 7 | |
11 gru 20:48
Eta:
bez "krzaków"
N={1,3,5,7,9} , P={4,6}
liczba trzycyfrowa parzysta :
NPP, NNP, PNP ( nie może być PPP, bo tylko dwie cyfry w tym zbiorze są parzyste
NPP = 5*2*1=10
NNP= 5*4*2= 40
PNP= 2*5*1= 10
R−m 60 takich liczb
11 gru 21:58
