trygonometria evciq: Funkcja f określona w zbiorze <0;4π>, dana jest wzorem f(x)=cos² x−sinx * |sinx|. Naszkicuj wykres funkcji f. Doszłam do tego, że: { cos² x−sin² x f(x)= { {cos² x + sin² x f(x)={cos2x { 1 Tylko co dalej Bardzo proszę o pomoc !

evciq: heeej... ?! może mi ktoś pomóc

Sabin: dokładniej: f(x) = cos2x dla x∊<0 ; π> ∪ <2π ; 3π> = 1 dla x∊(π ; 2π) ∪ (3π ; 4π> no i rysuj w podanych przedziałach... cos2x to tak jak cosinus, tylko dwa razy węższy, czyli np. jak cosx ma miejsce zerowe w π/2, tak cos2x będzie miał w π/4

evciq: oo a skąd wiadomo jakie są te dziedziny tego nie rozumiem

Sabin: Z wykresu sinusa Jak sobie narysujesz w układzie sinx na przedziale <0 ; 4π>, to widać, że sinx ≥ 0, czyli |sinx| = sinx dla x z pierwszych przedziałów, sinx < 0, czyli |sinx| = −sinx dla x z drugich przedziałów a stąd cała reszta.

evciq: yhmm.. No dobrze, ale tutaj jest wykres cosinusa, więc dlaczego mam rysować sinus

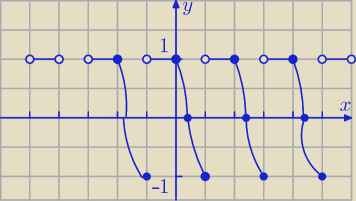
Godzio: f(x) = cos²x − sinx * |sinx| { = cos²x − sin²x dla x∊<2kπ,π+2kπ> f(x) { {= cos²x +sin²x dla x∊(π+2kπ,2π+2kπ) { = cos2x dla x∊<2kπ,π+2kπ> f(x) { {= 1 dla x∊(π+2kπ,2π+2kπ) (jedna jednostka na OX to π) Mysle że to powinno wyglądać jakoś tak

evciq: a skoro to jest cos2x to nie powinno być miejsce zerowe ^π₄ ?

evciq: Dziękuję bardzo za pomoc ja po prostu nie rozumiem na jakiej podstawie ta dziedzina jest wyznaczana:(

Godzio: sinx < 0 dla x∊(π+2kπ,2π+2kπ) w tym przedziale wykres znajduje sie ponizej OX sinx ≥ 0 dla x∊<2kπ,π+2kπ> analogicznie tyle ze powyzej OX

	π
a miejsca zerowe owszem są w		,
	4

okres o który mi chodziło (π) to chodziło co kwadracik

evciq: czyli przedziały zależą od wykresu sinusa, bo on może się zmieniać(być + lub −) tak? ale rysuję cos heh. o to chodzi, tak

Sabin: Tak, dokładnie o to chodziło (mi też)

evciq: aaaa nooo no to teraz wszystko jasne dzięki wielkie