Wyznaczyć lokalizację na budowę najkrótszego łączącego koryta kanału

Wyznaczyć lokalizację na budowę najkrótszego łączącego koryta kanału Dert: Koryta dwóch rzek mają przybliżony kształt krzywych y − x²=0 i x − y − 2 = 0. Wyznaczyć lokalizację na budowę najkrótszego łączącego je kanału. Napłodziłem takie coś: https://www.wolframalpha.com/input/?i=plot+y+%E2%88%92+x%5E2+%3D+0%2C+x+%E2%88%92+y+%E2%88%92+2+%3D+0%2C+-2x%3D0%2C+y%3D1%2C+y%3D-x%2B1

	3		1
I dwa punkty, które będą rozpoczynały kanał: P₁(		, −		),
	2		2

	−1−√5		3
P₂=(		, −		−√5)
	2		2

Czy to jest dobre rozwiązanie? Dodam, iż zadanie otrzymałem w liście "Pochodne cząstkowe funkcji dwóch i trzech zmiennych. Różniczka zupełna. Ekstrema funkcji dwóch i trzech zmiennych."

11 gru 16:36

Dert: Dodam, iż x − y − 2 = 0 i −2x=0 to pochodne cząstkowe funkcji y=x²

11 gru 16:37

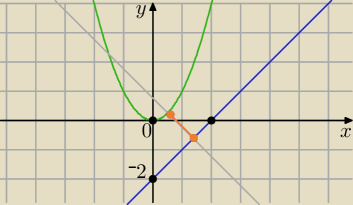
jc: Poszukajmy prostej, równoległej do danej prostej, stycznej do paraboli. y=x², y=x−2 Porównujemy pochodne. 2x=1 x=1/2, y=1/4 to współrzędne punktu na paraboli. Połączenie będzie prostopadłe do danej prostej. y=−x+b, 1/2=−1/4+b, b=3/4 y=−x+3/4 y=x−2 2y=−11/4, y=−11/8, x=2+11/4=15/4 to współrzędne punktu na prostej. (sprawdź ostatnie rachunki).

11 gru 18:21

a7:

11 gru 18:38

Dert: Dziękuję. O proszę, czasami warto zrobić funkcję f(x).

11 gru 18:55

a7: 18:21 powinno być

	5		5		11
po dodaniu (I+II): 2y=−5/4 y=−		x=y+2 czyli x=−		+2=
	8		8		8

11 gru 18:58

jc: Dziękuję emotka

11 gru 19:07

a7:

11 gru 19:11