Geometria analityczna BoosterXS: Wyznacz zbiór punktów płaszczyzny, których odległość od prostej k: y=−3 i odległość od okręgu x² + (y−3)²=1 jest taka sama. Mamy okrąg o środku S(0,3) i promieniu 1, oraz stałą funkcję liniową y=−3 ale totalnie nie wiem jak z tym dalej ruszyć. Podpowie ktoś jak się za to zabrać?

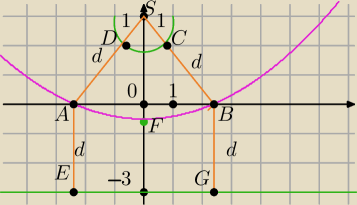
a7: F=(0,−1/2) parabola y=ax²−1/2 (b=0, gdyż x1+x2=0 −b/a=0 to b=0) BG=BS−1 B(x_B,0) G=(x_B,−3) √3²=√(x_B)²+9−1 ⇒ x_B=√7 A=(−√7,0) c/a=x₁*x₂=−√7*√7=−7 ⇒a=1/14

	1		1
y=		x2−
	14		2

a7:

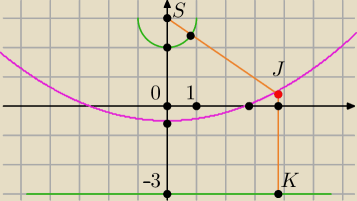
	1
spr. dla xJ=√14 yJ=1/2 J=(√14,		)
	2

JK=JS−1

	7		7		5		81		9		7
L=√(		)2=		P=JS−1=√(√14)2+(		)2 −1=√		−1=		−1=
	2		2		2		4		2		2

L=P