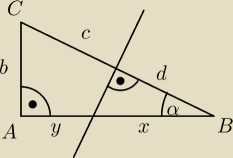
W trójkącie prostokątnym przyprostokątne mają długość 4cm oraz 6cm. Oblicz stosunek długości
odcinków, na jakie symetralna przeciwprostokątnej podzieliła dłuższą przyprostokątną tego
trójkąta.
c − długość przeciwprostokątnej
x+y=6
b=4
z twierdzenia Pitagorasa:
(x+y)2+b2=c2 ⇒ c=2√13
| c | ||
symetralna odcinka BC dzieli go na dwie równe części pod kątem prostym, zatem d= | =√13 | |
| 2 |
| x+y | 6 | 3√13 | ||||
cosα= | = | = | ||||
| c | 2√13 | 13 |
| d | √13 | |||
cosα= | = | |||
| x | x |
| 13 | 5 | |||
porównujemy prawe strony obu równań i otrzymujemy, że x= | , więc y= | |||
| 3 | 3 |
| x | 13 | 3 | 13 | ||||
= | * | = | |||||
| y | 3 | 5 | 5 |
| 13 | ||
13:5= | ||
| 5 |