Równanie wielomianowe
Mokry: Oblicz miejsce zerowe:
x3 + x + 1 = 0
Jakoś nic mi tu nie wychodzi
10 gru 17:53
ICSP: | | 1 | | 1 | | 4 + 27 | | 93 | |
Δ = |
| + |
| = |
| = |
| |
| | 27 | | 4 | | 62*3 | | 182 | |
x =
3√−1/2 + √Δ +
3√−1/2 − √Δ =
10 gru 17:57
Mila:
Równanie ma jedno rozwiązanie rzeczywiste.
f'(x)=3x2+1 ⇔funkcja f(x)=x3+x+1 jest rosnąca
Wzory Cardano, albo przybliżenie z własności Darboux.
10 gru 17:57
a7:
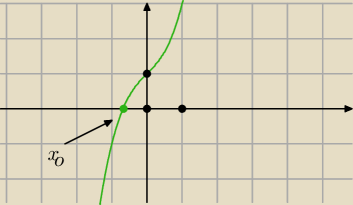
10 gru 17:59
Mariusz:
x
3 + x + 1 = 0
Zakładamy że rozwiązanie jest w postaci x=u+v
i wstawiamy do równania
Korzystamy z wzoru skróconego mnożenia a następnie grupujemy równanie
i zapisujemy je w postaci układu równań
(u+v)
3+(u+v)+1=0
u
3+3u
2v+3uv
2+v
3+(u+v)+1=0
| | 1 | |
u3+v3+1+3(u+v)(uv+ |
| )=0 |
| | 3 | |
u
3+v
3+1=0
Iloczyn będzie równy zero gdy co najmniej jeden z czynników będzie
równy zero jednak wcześniej założyliśmy że x = u + v
więc nie możemy czynnika u+v przyrównać do zera
u
3+v
3=−1
Przekształcamy powyższy układ równań tak aby uzyskać wzory Vieta
dla równania kwadratowego o pierwiastkach u
3 oraz v
3
u
3+v
3=−1
Teraz powyższy układ równań to wzory Vieta
dla równania kwadratowego o pierwiastkach u
3 oraz v
3
| | 1 | | √93 | | 1 | | √93 | |
(t+ |
| − |
| )(t+ |
| + |
| )=0 |
| | 2 | | 18 | | 2 | | 18 | |
| | −9+√93 | | −9−√93 | |
(t− |
| )(t− |
| )=0 |
| | 18 | | 18 | |
| | −108+12√93 | | −108−12√93 | |
(t− |
| )(t− |
| )=0 |
| | 216 | | 216 | |
| | 1 | |
x= |
| (3√−108+12√93+3√−108−12√93) |
| | 6 | |
11 gru 05:37
