nierówności wymierne salamandra:

	x2−8x+12
Czy przy rozwiązywaniu nierówności wymiernych np.		>=0, gdy odrzucę dziedzinę,
	x−3

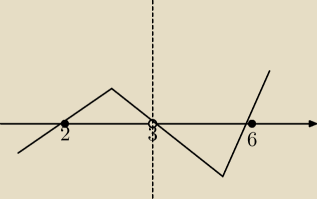
tj. x≠3, to przy rysowaniu wykresu tej funkcji pomijam ten x, czy uwzględniam go na rysunku, czyli wykres wyglądałby tak: I ostatecznym rozwiązaniem byłoby x∊<2;3) U <6; ∞)?

Szkolniak: Tak jak mówisz

Blee: tak wykres winien wyglądac zresztą wystarczy że przed rysowaniem przemnożysz obie strony nierówności przez (x−3)² i otrzymujesz piękny wielomian trzeciego stopnia

Szkolniak: Zawsze na końcu wyciągasz cześć wspólna tego co ci wychodzi i dziedziny Bo jeśli 3 należałoby do rozwiązania, to podstawiajac do nierówności, miałbyś dzielenie przez 0 − bez sensu

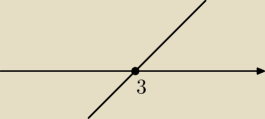
salamandra: Dzięki Natomiast gdybym miał już taką nierówność, gdzie miałbym załóżmy w pierwszym nawiasie funkcje kwadratowa bez miejsc zerowych, np.

(x2−x+1)
	>= 0, to wtedy rysuję po prostu
(x−3)

i x∊(3;∞)?

Blee: da