pierwiastki
salamandra: Liczba √11−6√2 jest równa:
a)√2−3
b)3−√2
c)1−3√2
d)3√2−1
Czy mogę to rozwiązywać po prostu przyrównując po kolei odpowiedzi? Zrobiłem to tak,
podstawiłem najpierw odpowiedź a), ale od razu ją odrzuciłem, gdyż jest < 0, a lewa strona jest
>=0,
następnie b)
√11−6√2 = 3−√2 / 2
11−6√2 = 9−6√2+2
2=2
8 gru 19:08
Blee:
to jest test ... możesz robić jak tylko uważasz ... istotne jest aby zaznaczyć dobrą odpowiedź
i zrobić to jak najszybciej
8 gru 19:12
Jolanta: (a−b)2=a2−2ab+b2
11=a2+b2
6√2=2ab
3√2=ab
a=3 b=√2
√(3−√2)2
8 gru 19:12
salamandra: Blee, bardziej pytałem o to, czy moja metoda jest dobra i nie prowadzi do jakichś ewentualnych
sprzeczności i wynik wyszedł przypadkowo (jedyne co wiem, ale to już mnei tutaj nauczyliście

, że przy podnoszeniu obustronnie do potęgi, obie strony musza byc dodatnie)
8 gru 19:23
Jerzy:
19:08 bardzo dobra interpretacja. Eliminujesz dwie odpowiedzi ujemne i sprawdzasz
prawdobodobną,bo widać, że ostatnia jest „za duża”
8 gru 19:37
Saizou : Na maturze jeszcze szybciej: wbijasz w kalkulator i porównujesz wyniki

Twoje rozumowanie jest takie.
Niech
√11−6√2=x (x>0, bo pierwiastek z liczby różnej od zera jest dodatni) / do kwadratu
11−6
√2=x
2
i teraz sprawdzasz wyniki, czyli podstawiasz za x kolejno odpowiedzi.
Wychodzi Ci że x = 3−
√2
8 gru 19:42
salamandra: Dzięki

A czy jest możliwość, aby rozwiązać takie zadanie algebraicznie? Gdzie nie szukałem, to
wszędzie rozwiązanie jest przedstawione za pomocą przekształcania wykresów, a ja rysować nie
lubię:
Ile maksymalnie rozwiązań może mieć równanie |||x|−3|−2| = m, gdzie m∊R
Próbowałem to rozbijać na zasadzie:
|||x|−3|−2| = m
||x|−3|−2 = m v ||x|−3|−2 =
−m
|x|−3−2 = m v |x|−3−2 = −m |x|−3−2= −m v
|x|−3−2 = m
x−3−2 = m v x−3−2 = −m x−3−2 = −m v x−3−2 = m x−3−2 = −m v x−3−2 = m
Tylko, że dostaje takiego oczopląsu, że nie wiem jak doprowadzić do ostatecznego rozwiązania,
nie zdziwię się, jak w rozbijaniu coś pominąłem
8 gru 19:55
ICSP: m ≥ 0
Wtedy
||x| − 3| = m + 2 v ||x| − 3| = m − 2 <− rozwiązania dla m ≥ 2
|x| = m + 5 v |x| = 1−m v |x| = m + 1 v |x| = 5−m <− rozwiązania dla m ≤ 1
x = m + 5 v x = −m − 5 v x = −m + 1 v x = m − 1 v x = m + 1 v x = −m − 1 v x = 5 − m v x = m −
5
Jak widać w najbardziej optymistycznym wypadku dostaniemy 8 rozwiązań.
Co znaczy najbardziej optymistyczny ? To znaczy m < 1 i też wspominane na początku m > 0
8 gru 20:07
ICSP: Poprawiam III linijkę.
||x| − 3| = m + 2 v ||x| − 3| = 2 − m <− rozwiązania dla m ≤ 2
Łatwo przy takich zapiskach coś s********ć
8 gru 20:09
8 gru 20:10
Saizou :
Dlatego łatwiej jest narysować funkcję po lewej stronie

8 gru 20:10
salamandra: A jaki jest algorytm przy wykonywaniu wykresu?
https://www.youtube.com/watch?v=nqvNl9xTRpQ
Dlaczego w początkowych fazach "−2" jest pominięte, a jak już jest uwzględniane, to wstępnie
bez wartości bezwzględnej?
8 gru 21:45
ICSP: Zaczynasz od wewnątrz i idziesz w kierunku zewnętrznym
1o Rysujesz |x|
2o Rysujesz |x| − 3
3o Rysujesz ||x| − 3|
4o Rysujesz ||x| − 3| − 2
5o Rysujesz |||x| − 3| − 2|
9 gru 11:04
ICSP:
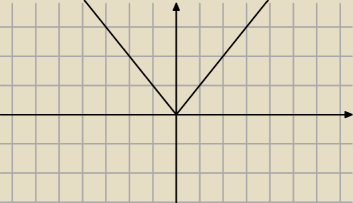
1
o
9 gru 11:05
ICSP:
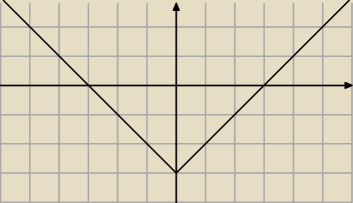
2
o
9 gru 11:05
ICSP:
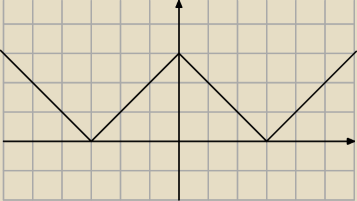
3
o
9 gru 11:07
ICSP:
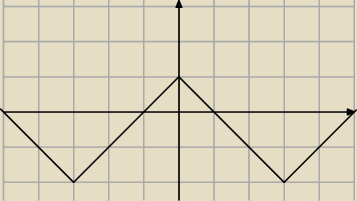
4
o
9 gru 11:07
ICSP:
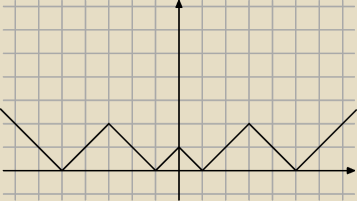
5
o
9 gru 11:08
salamandra: Dzięki

9 gru 12:40
 , że przy podnoszeniu obustronnie do potęgi, obie strony musza byc dodatnie)
, że przy podnoszeniu obustronnie do potęgi, obie strony musza byc dodatnie)
 Twoje rozumowanie jest takie.
Niech √11−6√2=x (x>0, bo pierwiastek z liczby różnej od zera jest dodatni) / do kwadratu
11−6√2=x2
i teraz sprawdzasz wyniki, czyli podstawiasz za x kolejno odpowiedzi.
Wychodzi Ci że x = 3−√2
Twoje rozumowanie jest takie.
Niech √11−6√2=x (x>0, bo pierwiastek z liczby różnej od zera jest dodatni) / do kwadratu
11−6√2=x2
i teraz sprawdzasz wyniki, czyli podstawiasz za x kolejno odpowiedzi.
Wychodzi Ci że x = 3−√2
 A czy jest możliwość, aby rozwiązać takie zadanie algebraicznie? Gdzie nie szukałem, to
wszędzie rozwiązanie jest przedstawione za pomocą przekształcania wykresów, a ja rysować nie
lubię:
Ile maksymalnie rozwiązań może mieć równanie |||x|−3|−2| = m, gdzie m∊R
Próbowałem to rozbijać na zasadzie:
|||x|−3|−2| = m
||x|−3|−2 = m v ||x|−3|−2 =
−m
|x|−3−2 = m v |x|−3−2 = −m |x|−3−2= −m v
|x|−3−2 = m
x−3−2 = m v x−3−2 = −m x−3−2 = −m v x−3−2 = m x−3−2 = −m v x−3−2 = m
Tylko, że dostaje takiego oczopląsu, że nie wiem jak doprowadzić do ostatecznego rozwiązania,
nie zdziwię się, jak w rozbijaniu coś pominąłem
A czy jest możliwość, aby rozwiązać takie zadanie algebraicznie? Gdzie nie szukałem, to
wszędzie rozwiązanie jest przedstawione za pomocą przekształcania wykresów, a ja rysować nie
lubię:
Ile maksymalnie rozwiązań może mieć równanie |||x|−3|−2| = m, gdzie m∊R
Próbowałem to rozbijać na zasadzie:
|||x|−3|−2| = m
||x|−3|−2 = m v ||x|−3|−2 =
−m
|x|−3−2 = m v |x|−3−2 = −m |x|−3−2= −m v
|x|−3−2 = m
x−3−2 = m v x−3−2 = −m x−3−2 = −m v x−3−2 = m x−3−2 = −m v x−3−2 = m
Tylko, że dostaje takiego oczopląsu, że nie wiem jak doprowadzić do ostatecznego rozwiązania,
nie zdziwię się, jak w rozbijaniu coś pominąłem

 1o
1o
 2o
2o
 3o
3o
 4o
4o
 5o
5o
