Oblicz pole powierzchni bocznej ostrosłupa. Kama: Podstawą ostrosłupa prostego jest trójkąt równoramienny o podstawie a długości 6cm. Krawędzie boczne b mają długość 5cm, a kąt dwuścienny między przystającymi ścianami ma miarę 60 stopni. Oblicz pole powierzchni bocznej tego ostrosłupa. Prosiłabym serdecznie o prawidłowe rozwiązanie zadanie, ale także łopatologiczne wyjaśnienie, co i jak, ponieważ zupełnie nie ogarniam tego działu. Z góry ślicznie dziękuję! <3

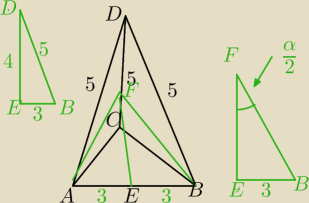
a7: kąt dwuścienny AFB to kąt między wysokościami ścian bocznych ACD i BCD

	|EB|
α/2=30 sin30=1/2		=1/2 czyli FB=2*3=6
	|FB|

pole powierzchni bocznej to suma trzech trójkątów

	1		1
2*PΔDCB+PΔABD=2*		*5*6+		*6*4=........
	2		2

a7: jeśli coś zbyt skrótowo to daj znać

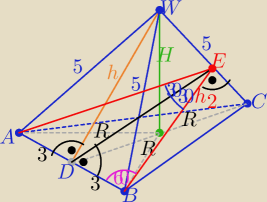
a@b: Jeżeli wszystkie krawędzie boczne mają taką samą długość, to spodek wysokości ostrosłupa pokrywa się ze środkiem okręgu opisanego na podstawie Z trójkąta prostokątnego BDW o kątach ostrych 30^o,60^o h=4 kąt dwuścienny między ścianami BCW i ACW to kąt AEB=60^o to z trójkąta prostokątnego DBE o kątach ostrych 30^o,60^o h₂=6

	1		1
Pb= P(ABW)+2P(BCW) =		*|AB|*h +		|CW|*h2
	2		2

	1		1
Pb=		*6*4+		*5*6=...........
	2		2

a7: a@b trzeba dodać dwa trójkąty BCW

a@b: We wzorze wpisałam , a później pominęłam przez nieuwagę Dzięki za zwrócenie uwagi

a7: no chyba to mój "debiut" w tym temacie (znajdywania w Twoich rozwiązaniach chochlików)

a@b: