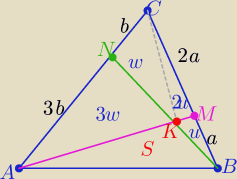
 1/ rys. zgodny z treścią zadania
2/ pola odpowiednich trójkątów oznaczyłam : u, 2u, w, 3w i P(ABK)= S
Dlaczego tak? ..... odpowiedz sam/a
to:
2(u+S)=4w+2u ⇒ 2S=4w oraz 3(w+3u)=3w+S ⇒ S=9u
1/ rys. zgodny z treścią zadania
2/ pola odpowiednich trójkątów oznaczyłam : u, 2u, w, 3w i P(ABK)= S
Dlaczego tak? ..... odpowiedz sam/a
to:
2(u+S)=4w+2u ⇒ 2S=4w oraz 3(w+3u)=3w+S ⇒ S=9u
| S | 10S | |||
P(ABC)=P= 4w+3u+S = 2S+ | +S ⇒ P= | ⇒ S=0,3P | ||
| 3 | 3 |
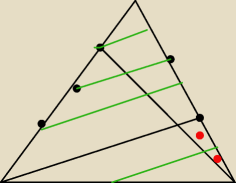 Pole trójkąta z czerwonymi kropkami = 1/3 * (2/5) * 1/4 = 1/30
Szukane pole = 1/3 − 1/30=9/30=1/10
Pole trójkąta z czerwonymi kropkami = 1/3 * (2/5) * 1/4 = 1/30
Szukane pole = 1/3 − 1/30=9/30=1/10


