Geometria Kuba152: W trójkącie prostokątnym ABC kąt BAC jest prosty. Punkt D należy do boku BC, przy czym BD=2CD. Z punktu B prowadzimy prosta prostopadłą do prostej AD, punkt E jest punktem przecięcia tych dwóch prostych. Wyznacz miarę kąta CED.

Kuba152: przepraszam pomyłka ABC jest równoramienny

a@b: @Kuba Masz wyznaczyć miarę kąta CED? czy tangens kąta CED ?

Mila: Kuba coś modyfikuje z treścią. To jest zadanie konkursowe.

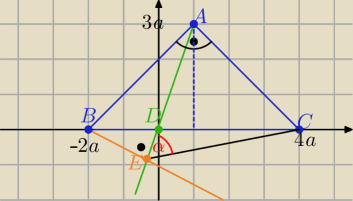
a@b: Analitycznie: A(0,3a) , B(−2a,0), C(4a,0) D(0,0) Szukany kąt α −− kąt między prostymi AE i EC

	1
prosta AE: y=3x prosta BE : y=−		(x+2a)
	3

	1		2
BE: y=−		x−		a
	3		3

Rozwiązując układ równań danych prostymi AE i BE otrzymamy współrzędne punktu E( −a/5, −3a/5)

	|a1−a2|
tgα=
	|1+a1*a2|

gdzie a₁ −− współczynnik kierunkowy prostej AE ⇒ a₁=3 a₂ −− współczynnik kierunkowy prostej EC

	3   a 5
to a2=		⇒ a2=1/7
	1   4a+ a   5

	|3−17|
zatem tgα=		⇒ tgα= 2
	|1+37|

to α≈63^o

a@b: Ech .. źle przeczytałam treść miało być : BD=2CD

a@b: Popraw dane na rysunku i obliczenia analogicznie jak wyżej Odp: α= 45^o

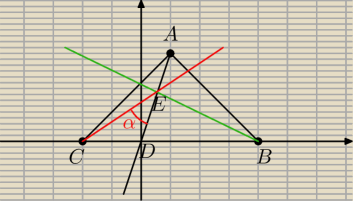
a7: na podstawie postu a@b A(a,3a) B(4a,0) C(−2a,0) D(0,0) prosta AD: y=3x prosta BE:y=−1/3x+2a

	3		9
punkt E=(		a,		a)
	5		5

prosta EC: a₂=9/13 tgα=U{|3−9/13|}{1+3*9/13)=3/4 α≈37^o

a@b:

	1
BE : y=−		(x−4a)
	3

a@b:

	2		6
to E(		,		)
	5		5

a@b: Możesz dokończyć ......bo mnie już się nie chce liczyć

a7: ale nie rozumiem czemu BE:y=−1/3(x−4a)

a@b: Bez straty ogólności można pominąć "a" B(4,0) to BE ⊥AD

	1
zatem BE: y=−		(x−xB)
	3

jasne?

a@b: Czemu nie rysujesz takiego układu?

a7: niestety nie, no ale trudno

a7: 01:53 bo nie umiem, nie wiem jak

a@b: tylko taki "pokręcony"

a7: zawsze mi wychodzi jakiś inny nie wiem jak to zrobić, zeby taki wychodził

a7:

a@b: To łatwe ... naucz się (dasz radę Rozciągaj kratki tak by były kwadracikami

a7: o już się udało dzięki

a@b:

a@b: Prosta przechodząca przez punkt B(x_o,y_o) o danym współczynniku kierunkowym "a" ma równanie: y= a(x−x_o)+y_o w tym zadaniu: a= −1/3 B(4,0)

	1
to BE: y=−		(x−4)+0
	3

	1		4
BE: y= −		x−
	3		3

a7: no dobra, ale czemu BE y= −1/3 (x−x_B) co to za wzór? nie znam

a7: no tak teraz mnie oświeciło

a7: dzięki

a@b: Napisałam wyżej

a@b: Dobranoc

a@b: Poprawiam zapis

	1		4
BE : y= −		x+
	3		3

a7: dzięki dobranoc, też już idę

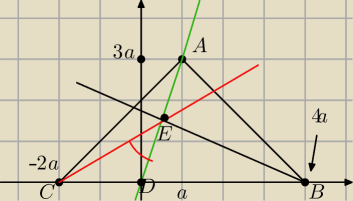
a7: punkty A(a,3a) B(4a,0) C(−2a,0) D(0,0) prosta AD: y=3x

	1		4
prosta BE: y=−		x+
	3		3

	2		6
punkt E (		a,		a)
	5		5

	1
prosta CE: y=		x+a
	2

	1   |3− |   2
tgα=		=1 czyli α=45o
	1+3*12

a@b: No i pięknie ( nawet i rysunek

a7:

Mila: 1)Rozwiązałam, podobnie jak Wy, z tym, że wierzchołek A umieściłam w punkcie (0,0) 2) Rozwiązałam też inaczej, ale trochę rachunków, chociaż nic trudnego. ( Jeżeli A7 chce zobaczyć, to wyślę rozwiązanie) 3) To jest zadanie konkursowe i musi być inny sposób. Chciałabym , aby Kuba napisał z jakiego to poziomu jest konkurs.

a7: ja chętnie bym zobaczyła

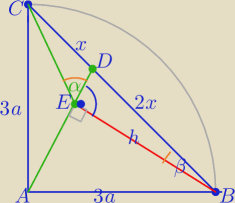
Mila: 1) |BC|=3a√2 x=a√2 2x=2a√2 |AD|²=(3a)²+(2a√2)²−2*3a*2a *√2 cos 45^o |AD|²=5a², [N[|AD|=a√5 2)

	9a2
PABC=		i PADB=3a2
	2

	1		1
PADB=		|AD|*h⇔		|AD|*h=3a2
	2		2

	6a
h=
	√5

======= 3) W ΔBED:

	h		3
cosβ=		⇔cosβ=
	|DB|		√10

	4a2
Z tw. Pitagorasa: |ED|2=
	5

	2a
|ED|=
	√5

W ΔCEB:

	18a2
|CE|2=h2+|BC|2−2h*|BC|*cosβ⇔|CE|2=
	5

	3a√10
|CE|=
	5

4) W CED: x²=|CE|²+|ED|²−2|CE|*|ED|*cosα

	18a2		4a2		3a√10		2a
(a√2)2=		+		−2*		*		*cosα
	5		5		5		√5

	22a2		12√2
2a2=		−		*a2cosα
	5		5

	1		√2
cosα=		=
	√2		2

α=45^o =====

a7: super

a7: wow

Mila:

Kuba152: Dziękuję Wam wszystkim !

a7: @Kuba152 Mila pisała, żebyś napisał z jakiego to konkursu z jakiego poziomu itp.

Kuba152: XVIII Warmińsko−Mazurskie Zawody Matematyczne Eliminacje − cykl grudzień Poziom: szkoły ponadpodstawowe