Zadanie optymalizacyjne 52 : Zadanie optymalizacyjne: Na słupie zawieszono termometr o długości 1 metra, który zajmuje miejsce między trzecim a czwartym metrem tego słupa, licząc od gruntu. W jakiej odległości od słupa powinien stanąć człowiek, który ma oczy na poziomie 1,70 metra, aby widzieć ten termometr pod możliwie największym kątem? (Przez kąt widzenia rozumiemy tu kąt, którego wierzchołkiem jest źrenica patrzącego, a ramiona przechodzą przez końce termometru. Pomoże ktoś zacząć? Zupełnie nie mam pomysłu.

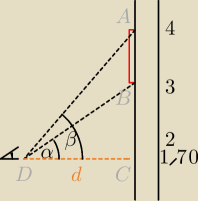
ite: Można ten kąt przedstawić jako różnicę β−α. tg α i tg β da się wyliczyć z ΔDCB i ΔDCA .

52 :

	3−1,7		1,3
tg α =		=
	d		d

	4−1,7		2,3
tg β =		=
	d		d

Wyszło mi, że

	d
tg (β−α)=
	d2−2,99

I teraz trzeba ułożyć wzór funkcji? Tylko nie wiem jak

52 :

	3−1,7		1,3
tg α =		=
	d		d

	4−1,7		2,3
tg β =		=
	d		d

Wyszło mi, że

	d
tg (β−α)=
	d2−2,99

I teraz trzeba ułożyć wzór funkcji? Tylko nie wiem jak

ite:

	d
Sprawdź wynik tg (β−α) =		.
	d2−2,99

Wygląda podejrzanie, nie ma powodu, żeby nie można było patrzeć na ten termometr z odległości 2,99 m.

ite: *z odległości √2,99 m.

ite: Jak poprawisz ten ułamek, to wynik będzie funkcją f(d) wyrażającą zależność kąta widzenia termometru od odległości patrzącego od słupa. Trzeba określić dziedzinę (d≥0) i zbadać ekstrema funkcji.

52 :

	2,3   1,3   − d   d		1   d		d
tg(β−α)=		=		=
	1,3*2,3   1−   d2		2,99   1−   d2		d2−2,99

Coś takiego mam

ite: We wzorze na tangens różnicy kątów w mianowniku jest suma.

52 : Racja, mój błąd

52 :

	d
f(d)=
	d2+2,99

	2,99
f'(d)=
	(d2+2,99)2

f'(d)=0

2,99
	=0
(d2+2,99)2

Na razie jest dobrze?

ite: Źle policzona jest ta pochodna: https://www.wolframalpha.com/input/?i=d%2F%28d%5E2%2B2.99%29 Tak na marginesie to równanie z 22:21 nie ma rozwiązań.

52 : Faktycznie

	2,99−d2
f'(d)=
	(d2+2,99)2

f'(d)=0

2,99−d2
	=0
(d2+2,99)2

2,99−d²=0 d>0 d=√2,99 Tak?

ite: Zgadza się. I dziedzina d>0 jest sensowniejsza, bo mój warunek d≥0 oznaczał, że obserwatorowi termometr może wpaść do oka a tego lepiej unikać.

52 : Ok. Dziękuję bardzo za pomoc