 W czworokątnym graniastosłupie prawidłowym przekątna podstawy równa
się d i tworzy z przekątną ściany bocznej kąt α. Oblicz objętość graniastosłupa.
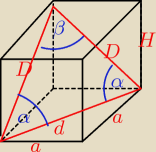
W czworokątnym graniastosłupie prawidłowym przekątna podstawy równa
się d i tworzy z przekątną ściany bocznej kąt α. Oblicz objętość graniastosłupa.
 a2+a2=d2
2a2 = d2
a2+a2=d2
2a2 = d2
| d2 | ||
a2 = | ||
| 2 |
| d | d√2 | |||
a = | = | |||
| √2 | 2 |
| sinβ | sinα | ||
= | |||
| d | D |
| d*sinα | d*sinα | |||
D = | = | = | ||
| sinβ | sin(180−2α) |
| d*sinα | d*sinα | ||
= | |||
| sin2α | 2sinαcosα |
| d | ||
D = | ||
| 2cosα |
| d2 | d2 | ||
+H2 = | |||
| 2 | 4cos2α |
| 1 | 1 | |||
H2 = d2*[ | − | } ] | ||
| 4cos2α | 2 |
| 1−2cos2α | ||
H2 = d2* | ||
| 4cos2α |
| cos2α | ||
H2 = d2* | ||
| 4cos2α |
| d√cos2α | ||
H = | ||
| 2cosα |
| d2 | d√cos2α | |||
V = a2*H = | * | = | ||
| 2 | 2cosα |
| d3√cos2α | |
| 4cosα |