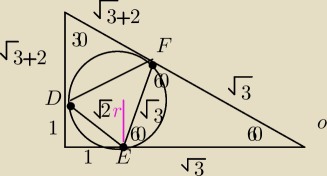
trójkąty salamandra: W trójkąt ABC, którego miary kątów są w stosunku 1:2:3, wpisano okrąg o promieniu 1. Oblicz: a) miary kątów trójkąta ABC, b) długosci boków trójkąta ABC, c) pole trojkąta DEF, gdzie punkty D,E,F są punktami styczności okręgu i boków a i b mam zrobione, problem mam z c), stanąłem w tym miejscu:

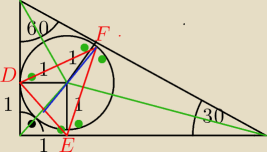
a7: DE=a=√2 DF=EF=√3 h²=(p[3})²−(p{2]/2)²=3−1/2−5/2 h=√⁵₂

	√5
liczymy P=1/2 ah P=1/2√2*√52=
	2

salamandra: Skąd wiadomo, że DF i EF są równe?

a7: racja nie są równe ∡FDE=75^o PΔ=1/2absin75^o=1/2*√2*√3*sin75^o≈1/2√6*0,9659≈....

salamandra: dzięki

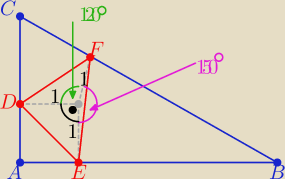
a@b: |∡EOD|=90^o , |∡EOF|=150^o , |∡DOF|=120^o

	1		1		1
P=		*1*1+		*1*1*sin120o+		*1*1*sin150o
	2		2		2

	3+√3
P=
	4

salamandra: Niestety to, to kompletnie nie wiem skąd wynika, być może jeszcze nie doszedłem do takich tematów na lekcji

a7: a@b zsumowała trzy trójkąty "składowe" trójkąta DEF sumując pole trzy razy użyła wzoru 1/2 ab*sinα a*b to zawsze 1*1 bo boki są zawsze 1, a sinusy raz to 90 sin90=1 sin 120=cos30 sin 150 =cos60

a@b: ΔDFC −− równoboczny czworokąt DOFC ma dwa katy proste w punktach styczności to kąt DOF=120^o zatem kąt EOF= 360^o−(120^o+90^o) = 150^o i liczysz pola trzech trójkątów (DOE i DOF i EOF) ,które tworzą trójkąt DEF Czy teraz jasne?

a7:

	√3
czyli mamy P1=1/2*1*1=1/2 P2=1/2*1*1*		=√3/4 P3=1/2*1*1*1/2=1/4
	2

	√3		3+√3
P=P1+P2+P3=1/2+√3/4+1=2/4+1/4+		=3/4+√3/4=
	4		4

a@b: Takie rachunki .... maturzysta sam powinien wykonać

salamandra: U mnie po prostu EFB był równoboczny na rysunku, a nie DFC

salamandra: Ok, a teraz mam zadanie: Boki trójkąta mają długości 13,14,15 − oblicz wartość sinusa największego kąta tego trójkąta. Domyśliłem się już jak, tj. P = 84 (ze wzoru Herona)

	1
P =		*a*b*sin α
	2

	1
84 = 13*14*		* sin α
	2

84
	= sinα
91

12
	= sinα
13

Skąd mam wiedzieć, który kąt jest największy, przy której parze boków, jest na to jakaś zasada?

a@b: Naprzeciw najdłuższego boku leży kąt który ma największą miarę

salamandra: Czyli krótko mówiąc ten, który nie ma z najdłuższym bokiem "kontaktu"?

a7: tak

a@b: 2 sposób Z tw. kosinusów

	132+142−152		5
cosα=		= .... =		( cosα>0 to α −− kąt ostry
	2*13*14		13

	12
to sinα = √1−cos2α= .... =
	13

salamandra: Twierdzenie cosinusów dopiero przede mna

a@b: ok