| 1 | 1 | 1 | ||||
Wykaż,że | = | + | ||||
| r | a | b |
| 1 | 1 | 1 | |||
= | + | ||||
| r | a | b |
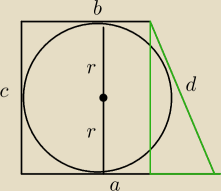c=2r
d=√4r2+(a−b)2
a+b=c+d
ab−2r={4r2+(a−b)2}
(a+b)2−4r(a+b)+4r2=4r2+(a−b)2
4ab=4r(a+b)
1/r=(a+b)/ab
1r=1a+1b
====================
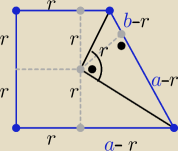
| ab | 1 | a+b | ||||
r2=(a−r)(b−r) ⇒ ab=r(a+b) ⇒ r= | ⇒ | = | ||||
| a+b | r | ab |
| 1 | 1 | 1 | ||||
to: | = | + | ||||
| r | a | b |