Dział - Geometria analityczna qwertyuiop: → W trójkącie ABC dane są: A(−3, −3), AB = [7, 0] oraz środek ciężkości S(3¹₃, −1¹₃). Oblicz miarę kąta rozwartego ABC tego trójkąta. W odpowiedziach jest: 135 stopni. Sam wyliczyłem współrzędnie trókąta B(4, −3) i C(9, 2) i teraz nie wiem co dalej. Proszę o wyjaśnienie.

Leszek: Z iloczynu skalarnego wektorow BA i BC , cos α = ........

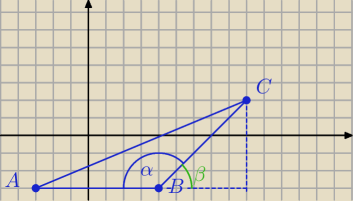
janek191: Oblicz β, a następnie α.

janek191:

	2 −(−3)
tg β =		= 1
	9 − 4

β = 45^o α = 180^o − 45^o = 135^o

a@b:

	5kratek
@janek tgβ =		=1 ⇒ β=45o
	5 kratek

α=135^o

janek191: ETA ?

Leszek: Zadania z geometrii analitycznej rozwiazujemy na podstawie danych liczbowych podanych w zadaniu a nie na podstawie rysunku i " kratek" Na maturze taki sposob nie bedzie uznany !

qwertyuiop: Dzięki za rysunek janek. Rozjaśnił mi jak to zrobić to zadanie. Sam policzyłem i się zgadza z waszymi rozwiązaniami. Jeszcze raz dzięki.

maturka: @Leszek .... piszesz bzdury

Leszek: Jak uczen nie zna iloczynu skalarnego wektorow to nalezy napisac rownanie prostej BC , wyznaczy wspolczynnik kierunkowy a , czyli tg β = a ⇒ β = ..... i nastepnie α = ... jako kat dopelniajacy .

maturka: Moja Pani mówiła,że też tak można, uzasadniając że wierzchołki są punktami kratowymi

Leszek: To ewentualnie w profilu podstawowym , ale nie w profilu rozszerzonym !