Szkicowanie funkcji wymiernej
Patryk: Witam,
Czy mógłby mi ktoś wytłumaczyć jak naszkicować wykres takiej funkcji wymiernej? Gdy szkicowałem
funkcję gdzie cały wzór był pod modułem to było proste bo wszystko co poniżej 0 odbijałem, ale
w tym przykładzie moduł mam w mianowniku. Rozważyłem jak dotąd dwa przypadki i mam dwa różne
wzory i dwie asymptoty pionowe.
|x| − 3 = 0
x = 3 lub x = −3 // asymptoty
Dla x ≥ 0
Dla x < 0
4 gru 15:50
Jerzy:
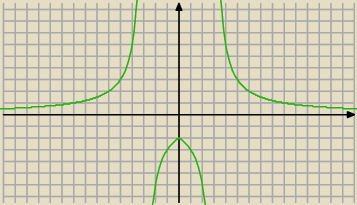
4 gru 15:51
Jerzy:
| | 6 | |
Dla x < 0 masz f(x) = − |
| |
| | x + 3 | |
4 gru 15:57
a@b:
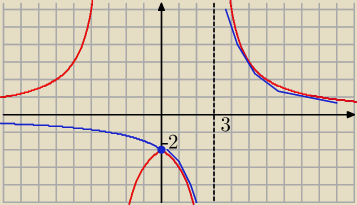
| | 6 | |
1/ rysujesz wykres niebieski y= |
| |
| | x−3 | |
Punkt przecięcia niebieskiego wykresu z osią OY (0,−2)
2/ odbijasz wszystko co po prawej stronie na lewą wraz z wykresem po prawej
i to wszystko
4 gru 15:59
Jerzy:
Odbijasz , bo to jest funkcja parzysta, czyli: f(−x) = f(x) i wykres jest symetryczny względem
osi OY.
4 gru 16:01
a@b:
Jeszcze zapomniałam narysować odbitej asymptoty x= −3 ( po lewej stronie
4 gru 16:02
Patryk: Ok, dziękuję za rysunek. A gdyby cały mianownik był pod modułem to czym różnił by się wykres?
4 gru 16:10
Patryk: Bo może być wiele przypadków, np. licznik pod modułem, mianownik pod modułem i chciałbym
zrozumieć na czy polegała by różnica
4 gru 16:13
Jerzy:
Wtedy to co pod osią OX odbijasz nad oś.
4 gru 16:15
Jerzy:
| | 6 | |
To co napisałem dotyczy tej funkcji w postaci f(x) = |
| |
| | |x − 3| | |
4 gru 16:16

