Parametr, równanie Szkolniak: Określ liczbę rozwiązań równania w zależności od parametru m. |x|=m−|m|

	⎧	0, gdy m≥0
narysowałem funkcję f(x)=|x| oraz funkcję g(m)=m−|m|, gdzie g(m)=	⎩	2m, gdy m<0

i czy w takim razie będzie jedno rozwiązanie dla m∊{0} i 0 rozwiązań dla m∊R\{0}|?

Des: 1 rozwiązanie dla m ≥ 0 , dla m < 0 brak rozwiązań

ite: |x|=m−|m| https://www.geogebra.org/graphing/w44n6fg4 w animacji |x| kolor zielony m−|m| kolor czerwony

Szkolniak: W takim razie moje rozpisanie funkcji g jest nieprawidłowe? Bo z GeoGebry patrząc, jest to funkcja, której wykres jest równoległy do osi OX

Des: 1 rozwiązanie: m − |m| = 0 −−−−−−−−−−−−−−−−−−−−−−−−− dla m ≥ 0: m − m = 0 0 = 0 → tożsamość m ≥ 0 good −−−−−−−−−−−−−−−−−−−−−−−−− dla m < 0: m + m = 0 2m=0 m=0 ∉D not so good −−−−−−−−−−−−−−−−−−−−−−− −−−−−−−−−−−−−−−−−−−−−−− 2 rozwiązania: m − |m| > 0 dla m ≥ 0: m − m > 0 0>0 sprzeczność not good −−−−−−−−−−−−−−−−−−−−−−− dla m < 0: m+m>0 2m>0 m>0 ∉D not so good

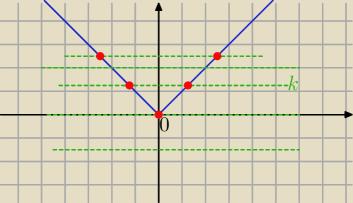
a@b: k=m−|m| 1 rozwiązanie dla k=0⇒ m−|m|=0 ⇒ m≥0 0 rozwiązań dla k<0 ⇒ m−|m|<0 ⇒ m<0

Szkolniak: Teraz już wszystko jasne, dzięki za wytłumaczenie