Dlaczego funkcja nie posiada punktów przegięcia
Holtz: Dlaczego funkcja nie posiada punktów przecięcia?:
| | −6x4+4x2+2 | |
Jej pochodna drugiego stopnia wynosi: |
| |
| | (1−x2)4 | |
Dlaczego wykres takiego wielomianu jest dziwny, tzn. podniesiony w zerze?
2 gru 14:48
Holtz: Pierwiastki tego wielomianu w liczniku pochodnej wyszły 1 i −1
2 gru 14:48
Jerzy:
Bo druga pochodna nie ma miejsc zerowych.
2 gru 14:50
Szkolniak: Zwróć uwagę na dziedzinę
2 gru 14:50
Jerzy:
| | 2(3x2 + 1) | |
f"(x) = |
| |
| | (1 − x2)3 | |
2 gru 14:51
Jerzy:
f"(x) ≠ 0 dla dowolnego x.
2 gru 14:52
Jerzy:
Kiepsko policzyłeś drugą pochodną.
2 gru 14:52
a@b:
Ułamek jest równy zero ⇔ gdy licznik=0
zatem 1 ≠0
wniosek: ...........
2 gru 14:53
Blee:
aż dziwne że nikogo nie zainteresowało czym są:
punkty
przecięcia 
2 gru 15:02
a@b:
"przecięcia" nożem ? ziemniaka na pół ;
2 gru 15:18
Holtz: Nie widzę rozwiązania
2 gru 19:16
Holtz: Przecież pochodna ma pierwiastki.
2 gru 19:17
a7: 14:53 a@b napisała przecież, że druga pochodna nie będzie równa zero dlatego nie ma punktów
przeg(c)ięcia
a 14:51 Jerzy wyznaczył prawidłowo drugą pochodną 3x2 +1 jest zawsze większe od zera
pomnożone przez dwa tym bardziej więc licznik jest zawsze większy od zera więc nie ma punktów
przegięcia?
2 gru 19:20
Jerzy:
Oprzytomniej.Licznik jest zawsze dodatni.
2 gru 19:20
a7: tzn. ja się nie znam, ale tak zrozumiałam to, co napisali poprzednicy
2 gru 19:21
a7: no właśnie Jerzy potwierdza
2 gru 19:21
Holtz: Aha, faktycznie!
A to ciekawe, jeżeli nie rozłożę licznika to normalnie wychodzą pierwiastki, dlaczego?
2 gru 19:23
Jerzy:
Dla uściślenia,druga pochodna się nie zeruje,a to warunek konieczny istnienia punktu
przegięcia.
2 gru 19:24
Jerzy:
Nie pisz glupot, masz złą drugą pochodną.
2 gru 19:25
Holtz: Czy (6x2+2)(1−x2) równa się −6x4+4x2+2?
2 gru 19:32
jc: | 1 | | 1 | | 1 | | 1 | |
| = |
| ( |
| + |
| ) |
| 1−x2 | | 2 | | 1−x | | 1+x | |
| | 1 | | 1 | | 1 | | 2+6x2 | |
( |
| )''= |
| + |
| = |
| |
| | 1−x2 | | (1−x)3 | | (1+x)3 | | (1−x2)3 | |
2 gru 19:36
Holtz: Ja cały czas uważam, że mam dobrą f"(x)
2 gru 19:36
Holtz: Dzięki!
Czyli muszę zawsze skracać licznik z mianownikiem? Upraszczać wyrażenia? Bo bubel mi wychodzi
bez tego.
2 gru 19:39
a7: no to pokaż jak liczysz i może uda się znaleźć Twój błąd, bo jest
2 gru 19:39
Holtz: Dobrze
2 gru 19:40
jc: Masz dobrą pochodną.
2 gru 19:41
ABC:
teraz to zakręciliście człowieka, jeden mówi dobra pochodna, drugi zła
2 gru 19:43
a7: tak właśnie policzyłam pochodna jest dobra , sorki
2 gru 19:46
a7: może Jerzy ją przekształcił?
2 gru 19:47
a7: zobacz wykres funkcji i zauważ, że nie ma zmian w wypukłości funkcji (nie zmienia się z
wklęsłej na wypukłą nigdzie) (nie jest w ogóle ona ciągła) może tu jest pies pogrzebany ?
2 gru 19:53
2 gru 19:54
a7: bo ja już widzę, że funkcja (druga pochodna) nie spełnia warunków wypukłości ani wklęsłości,
więc nie może być punktów przegięcia
2 gru 19:55
Holtz:
| | 2(1−x2)2−(4x3−4x)2x | | 2(1−2x2+x4)−(8x4−8x2) | |
f"(x)= |
| = |
| |
| | (1−x2)4 | | (1−x2)4 | |
| | 2−4x2+2x4−8x4+8x2 | | −6x4+4x2+2 | |
= |
| = |
| |
| | (1−x2)4 | | (1−x)4 | |
2 gru 19:56
a7: tak obliczyłam tak samo
2 gru 19:57
Holtz:
Dziękuję. Z tego, co widzę w odpowiedziach, mogę ustalić przedziały gdzie funkcja f(x) jest
wklęsła, a gdzie wypukła. Jednak funkcja nie na punktów przegięcia, co dowodzi wykres drugiej
pochodnej.
Czyli muszę douczyć się, jak szkicować wykresy wielomianu, bo ten jest taki dziwny.
2 gru 20:04
a7: ale są dwie asymptoty pionowe zobacz wykres, i funkcja jest wypukła dla x∊(∞,−1) oraz dla
x∊(1,∞)
a wklęsła na przedziale (−1, 1) chyba dobrze mówię, i nie ma punktów przegięcia w ramach tych
przedziałów patrz definicja w linku
2 gru 20:05
Holtz: Aha, to ja jestem dziwny. Wykres jest trywialny.
2 gru 20:05
Holtz: Dziękuję już załapałem
2 gru 20:06
ABC:
na pytanie tytułowe ja bym odpowiedział tak:
funkcja nie posiada punktów przegięcia, bo jedyni kandydaci na te punkty przegięcia (x=−1 oraz
x=1) nie należą do dziedziny funkcji
2 gru 20:08
a7:
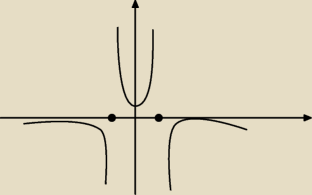
rysunek trochę poglądowy
2 gru 20:10
a@b:
"Świetny" jest ten rysunek
2 gru 20:14
ABC:
rysować każdy może trochę lepiej lub trochę gorzej
2 gru 20:14
a7: 
2 gru 20:15
a@b:
2 gru 20:16