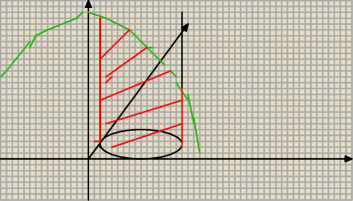
Objętość bryły Mateusz: Obliczyć objętość bryły ograniczonej płaszczyznami: z = 0 (x−1)² + y² = 1 ⇒r_w = 1 z = 9 − (x²−y²) ⇒ r_p = 3 więc będzie to okno vivianniego wycięte w paraboloidzie obrotowej. Interesuje nas obszar zaznaczony na czerwono. Ponieważ wycięta bryła to "ścięty" walec zastosujemy współrzędne walcowe. −pi/2≤α≤pi/2 0≤r_w≤1 0≤z≤9−(r_w)² czy dobrze dobrałem obszary całkowania

jc: To siodło, nie paraboloida. Poza tym, tylko jedna z powierzchni jest płaszczyzną. Wymienione powierzchnie rozcinają przestrzeń na pewną liczbę obszarów. Skąd wiesz, które obszary wybrać? Lepiej, a na pewno ściślej, opisywać obszary nierównościami. Przykładowo, czy z bierzesz z≥0 czy z≤0?

jc: Dobrze masz. Ok, z rysunku wynika, że 0 ≤ z ≤ 9−x²−y² (myślę, że powyżej jest błąd w znaku) (x−1)²+y²≤1 x=r cos a y= r sin a 0 ≤ r ≤ 1 0 ≤ z ≤ 9−r² −π/2 ≤a ≤π/2