Matematyka dyskretna Kalasznikov: Udowodnij następującą własność:

	n k		2n n
∑nk=0		2=

Stawiam browara za pomoc

jc: Na ile sposobów możesz wybrać n elementowy podzbiór ze zbioru 2n elementowego? Oczywista odpowiedź jest po prawej stronie równość. Możesz też podzielić zbiór 2n elementowy na 2 równe podzbiory, a potem wybierać podzbiory n elementowe wybierając k elementów z pierwszgo podzbioru, a pozostałe n−k z drugiego, k=0,1,2,...,n. Mówi o tym suma po lewej stronie. Stąd równość.

AdamP: "Oczywista odpowiedź jest po prawej stronie równość." No tak, ale jestem w tym zielony ponieważ to moje jedne z pierwszych zajęć z tym tematem. Jak mam to udowodnić?

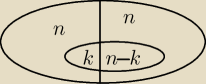
jc: Wybierasz n elementów ze zbioru 2n elementowego (rysunek). Zbiór 2n elementowy dzielisz wcześniej na 2 równoliczne podzbiory. Aby wybrać n elementów, wybierasz k elementów z lewego podzbioru, a pozostałe n−k z prawego. Dla danego k (k=0,1,2,...)

	n k	n n−k		n k
możesz to zrobić na			+		2 sposobów.

Sumujesz względem k i to samo, co byś miał wybierając od razu n elementów

	2n n
ze zbioru		elementowowego.

Oczywiście, co ważne, dla każdego dla różnych k otrzymujesz rozłączne rodziny podzbiorów.

jc: Tam zamiast + powinno być =, popraw sobie.