Proste i okręgi salamandra: Okrąg podzielono na trzy części w stosunku 7:8:9. Przez punkty podziału poprowadzono styczne, które przecięły się w punktach A, B, C. Uzasadnij, że kąty trójkąta ABC są równe 67,5, 60, 52,5

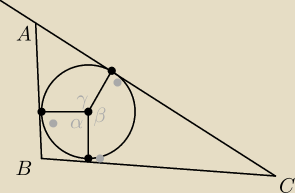
Saizou : TIP: wyznacz kąty α, β oraz γ

salamandra: zakładam że przy γ jest to "8", więc 8*15 = 120 α = 7*15 = 105 β = 135

Bleee: Bo tam w zadaniu powinno byc: W stosunku 47 : 48 : 49

Saizou : Tak jak pisze @Bleee wychodzą dobre wyniki dla tych danych Zasadę już masz, wiesz kwestia zmiany danych to nie problem

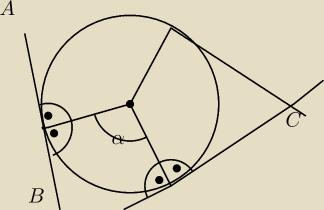
a7: 7+8+9=24 360/24=15 α,β,γ 105 stopni,120 stopni, 135 stopni kąt ABC=360−α−90−90 analogicznie ∡BCA=360−β−180 i ∡BAC=360−γ−180

a7: no rzeczywiście 47+48+49=144 360/144=2,5 α,β,γ równe 117,5 120 122,5 ∡ABC=360−180−117,5=62,5 ∡ BCA=360−180−120=60 ∡BAC=.....

a7: Czy potrzebne jakieś wyjaśnienie?

salamandra: Czyli jest błąd w treści? A dla tych danych jakie byłyby wyniki?

Bleee: Dla pierwotnych danych przecież wyznaczyła kąty α, β, γ teraz wystarczy zrobić 180−α, itd. i masz katy

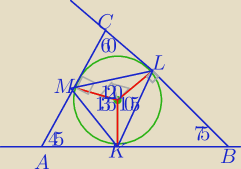
Mila: ∡K=60^o ∡L=67.5^o ∡M=52.5^o

salamandra: a te kąty KLM (rozumiem jako kąty między styczną a cięciwa), to nie będą tak jakby "na zewnątrz" trójkąta?

Mila: Kąty wewnętrzne ΔKLM wpisanego w okrąg.

salamandra: Zakładam, że kąt (L) między styczną a cięciwą (KL) jest dwa razy mniejszy od kąta środkowego opartego na tej cięciwie, więc wynosi 52,5. Analogicznie z kątami K i M, jednak są te kąty na zewnątrz trójkąta, jak zatem dojść do miary kątów wewnętrznych trójkąta KLM? Czyżby tak, że liczę też de facto miarę kąta (L) między styczną a cięciwą (LM), więc 60 stopni, i od 180 odejmuje dwa kąty między styczną a cięciwą czyli 180−52,5−60?

Mila: Oj, salamandra 1) Moje rozwiązanie nie odpowiada treści zadania, ale chciałam Ci pokazać, które kąty mają takie miary, jak w odpowiedzi. 2) ∡MKL− kąt wpisany oparty na cięciwie ML, której odpowiada kąt środkowy 120^o, zatem: ∡K=60^o Itd.