diagram Hassego Ketrys: Diagram Hassego. Mam narysować diagram Hassego dla iloczynu kartezjańskiego dzielników 5 i dzielników 10. Wiem jak to narysować, tylko pytanie jest takie, w jakiej kolejności od dołu na diagramie zapisywać pary liczb? bo muszę później wyznaczyć elementy maksymalne i minimalne bez (1,1) i (5,10) Pary liczb {(1,1),(1,2),(1,5),(1,10),(5,1),(5,2),(5,5),(5,10)}.

ite: A jaka relacja porządkuje ten zbiór?

Ketrys: (x, y) ≺ (z, t) ⇐⇒ x|z ∧ y|t

ite: Czy x,z,y,t są dowolnymi liczbami całkowitymi?

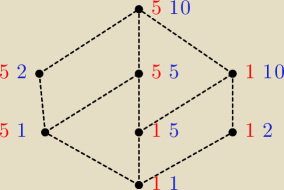
Adamm: spróbujmy wyznaczyć elementy minimalne w zbiorze X\{(1, 1), (5, 10)} mamy (1, 2), (1, 5), (5, 1) Teraz wyznaczmy elementy minimalne w zbiorze X\{(1, 1), (5, 10), (1, 2), (1, 5), (5, 1)} mamy (1,10), (5,2), (5,5) Nasz diagram będzie się składał z 4 stopni.

Adamm: Dodatkowo, możemy powiedzieć, że nasza krata nie jest modularna, bo mamy kopię kraty N₅ Faktycznie, {(1, 1), (1, 5), (5, 5), (5, 2), (5, 10)} ≡ N₅

Ketrys: okej, czyli dobrze to zrobiłem, dziękuje bardzo za pomoc.

Ketrys: a właściwie to (1,2) nie powinno być połączone też z (5,2)?

Adamm: tak, powinno, przepraszam

Ketrys: no w diagramach Hassego bardzo łatwo się pomylić jeszcze jedno pytanko, ograniczeniem dolnym zbioru {(5, 2),(1, 10)} jest (1,2) a górnym (5,10)?

Adamm: są dwa ograniczenia dolne (1, 1) oraz (1, 2) górnym jest faktycznie jedynie (5, 10)

Ketrys: rzeczywiście, czyli infimum tego zbioru to (1,2) a supremum (5,10)?

Adamm: tak