wykaż Kamil: Na okręgu o promieniu r opisano trapez, którego przekątne mają długość f i e Wykaż że zachodzi nierówność f²+e²≥16r² Bardzo proszę o pomoc

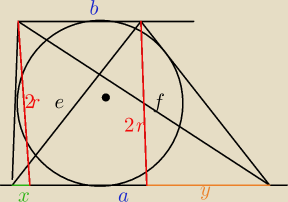
a7: mamy dwa trojkąty prostokatne i z tw Pitagorasa f²=(2r)²+(a−y)² e²=(2r)²+(a−b−y)² dodajemy f² do e² ⇒f²+e²≥4r², gdyż ((a−y)² większe równe od zera oraz (a−b−y)² większe równe zero

a7:

a7: błąd już poprawiam

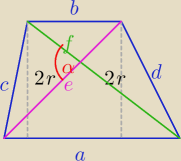
a@b: c≥2r i d≥2r to (c+d)≥4r

	fe		a+b
P=		*sinα i P=		*2r , dla α=90o pole jest największe
	2		2

	fe		a+b
zatem		≥		*2r oraz a+b= c+d ( z warunku wpisania okręgu w trapez
	2		2

to fe≥(a+b)*2r≥8r² oraz f²+e²≥ 2fe to: f²+e²≥16r² =============== c.n.w.

a@b: @a7 W treści nie jest powiedziane,że przekątne są prostopadłe ?

a7: nie no w ogóle moja koncepcja była błędna

a@b: Chyba,że ta czarna "kropa" na Twoim rys. ....oznacza środek okręgu

a7: tak, to środek okręgu, ale koncepcja i tak błędna i do niczego mnie ostatecznie nie doprowadziła...

a@b: