Python monety i kwota
Sara07: Mamy do dyspozycji monety o nominałach 5 i 9 oraz kwotę 34. Jak znaleźć najmniejszą ilość
monet, która zwróci tę kwotę. Jest to prawdopodobnie związane z problemem Frobeniusa
Jak napisac program w Pythonie aby rozwiać ten problem?
27 lis 22:30
Adamm:
najmniej będzie wtedy, kiedy będziemy mieli najwięcej dziewiątek
A to już jest łatwe
9+9+9 = 27, 34−27 = 7 nie pasuje
9+9 = 18, 34−18 = 16 nie pasuje
34−9 = 25 − pasuje
najmniej monet mamy wtedy, gdy mamy jedną dziewiątkę, i pięć piątek,
czyli sześć monet
27 lis 22:42
Adamm: byłoby ciekawsze, gdyby rozpatrywać np. 3 nominały
27 lis 22:43
Sara07: A jak napisac program zeby liczył najniejszą ilość założmy dla danych dwóch nominałow
nwd(x,y)=1 i danej kwoty?
27 lis 22:48
Adamm:
Ta kwota musi być odpowiednio duża.
Niech dana będzie liczba z. Możemy założyć, że x≥y.
z = kx+r dla 0≤r<x.
Jeśli y|r, to zakończone. (bo r = my, więc z = kx+my)
Jeśli nie, to zapisz z = (k−1)x+r dla pewnego r, i sprawdź czy y|r.
Tak do skutku. Z problemu Frobeniusa wiemy, że program zawsze zakończy się sukcesem
dla z≥(x−1)(y−1).
27 lis 23:18
Sara07: Czemu kwota ma być odpowiednio duża a np gdyby była 34

27 lis 23:29
Adamm:
No bo nie zawsze się taką liczbę da przedstawić za pomocą tych dwóch nominałów.
| | z | |
Po prostu szukamy k, takiego by y|(z−kx), k≤ |
| . |
| | x | |
27 lis 23:32
albi: def coins(starting
value, number1, number2):
if number2 > number1:
number2, number1 = number1, number2
for i in range(starting
value // number1, 0 , −1):
x = starting
value − number1 * i
if x % number2 == 0:
coin
n2 = x // number2
coin
n1 = i
return coin
n2 + coin
n1
Przykładowy program, ale oblicza to tylko dla odpowiedniej kwoty którą można rozłożyć na
podane nominały większe od 0, więcej mi się nie chce

27 lis 23:33
albi: Adamm Takie pytanko, bo napisałeś "Z problemu Frobeniusa wiemy, że program zawsze zakończy się
sukcesem
dla z≥(x−1)(y−1)"
Ja co prawda tego problemu nie znam ale jeżeli weźmiemy pod uwagę z = 7, x = 3, y = 2, to
założenie z≥(x−1)(y−1) jest spełnione ale 7 rozłożyć na 3 i 2 nie możemy. Mogę coś źle
rozumieć bo to z takiej szybkiej analizy
27 lis 23:39
Sara07: Ale dla (x,y)=(5,2) oraz 13 pokazuje zły wnik
27 lis 23:45
albi: Adamm nie ważne ja nie wiem co mówie dzisiaj, Sara wydaje mi się że pokazuje poprawnie, jaki
jest według Ciebie poprawna odpowiedź?
27 lis 23:52
Sara07: 3*5−1*2 czyli powinno być 4
27 lis 23:56
albi: Nie wiedziałem że bierzemy pod uwagę odejmowanie nominałów

Niestety dzisiaj już odpadam ale
liczę że dasz radę sama coś napisać, powodzenia
28 lis 00:00
Sara07: Tak niestety odejmowanie też

28 lis 00:10
Adamm:
27 lis 23:39
7 = 3+2*2
28 lis 08:49
Bleee:
Sara07 − że niby w którym momencie masz podane że 'odejmowanie tez'?
Podaj DOKLADNA treść zadania w takim razie.
28 lis 08:57
Adamm:
Po prostu trzeba równanie
z = ax+by rozwiązać w a, b
Znajdujemy jakiekolwiek rozwiązanie (a0, b0) za pomocą algorytmu Euklidesa.
(tzn., algorytm stosujemy do x, y, otrzymane współczynniki mnożymy przez z)
Wtedy wszystkie rozwiązania są dane przez:
a = a0+t*y, b = b0−t*x
Chcemy znaleźć mint∊Z (|a|+|b|).
28 lis 09:01
Adamm:
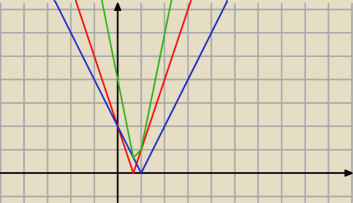
to jest problem optymalizacji
np. dla |3x−2| oraz |2x−2| mielibyśmy powyższy wykres (funkcja to |2x−2|+|3x−2|).
zauważ, że składa się on z 3 prostych, i tak będzie zawsze
|a| = 0 ⇒ a = 0 ⇒ t = t
1
|b| = 0 ⇒ b = 0 ⇒ t = t
2
(tu t
1, t
2 to pewne liczby wymierne)
W każdym razie możemy założyć t
1≤t
2.
wiadomo, że minimum będzie albo na przedziale [t
1, t
2] (w przypadku gdy zawiera
liczbę całkowitą), albo poza tym przedziałem, ale jak najbliżej niego, tzn.
minimum wynosi floor(t
1) lub ceil(t
2) (podłoga i sufit).
28 lis 09:23
Adamm:
znalezienie minimum na [t1, t2] nie jest trudne, bo funkcja ta jest tam liniowa.
28 lis 09:23


 Niestety dzisiaj już odpadam ale
liczę że dasz radę sama coś napisać, powodzenia
Niestety dzisiaj już odpadam ale
liczę że dasz radę sama coś napisać, powodzenia

 to jest problem optymalizacji
np. dla |3x−2| oraz |2x−2| mielibyśmy powyższy wykres (funkcja to |2x−2|+|3x−2|).
zauważ, że składa się on z 3 prostych, i tak będzie zawsze
|a| = 0 ⇒ a = 0 ⇒ t = t1
|b| = 0 ⇒ b = 0 ⇒ t = t2
(tu t1, t2 to pewne liczby wymierne)
W każdym razie możemy założyć t1≤t2.
wiadomo, że minimum będzie albo na przedziale [t1, t2] (w przypadku gdy zawiera
liczbę całkowitą), albo poza tym przedziałem, ale jak najbliżej niego, tzn.
minimum wynosi floor(t1) lub ceil(t2) (podłoga i sufit).
to jest problem optymalizacji
np. dla |3x−2| oraz |2x−2| mielibyśmy powyższy wykres (funkcja to |2x−2|+|3x−2|).
zauważ, że składa się on z 3 prostych, i tak będzie zawsze
|a| = 0 ⇒ a = 0 ⇒ t = t1
|b| = 0 ⇒ b = 0 ⇒ t = t2
(tu t1, t2 to pewne liczby wymierne)
W każdym razie możemy założyć t1≤t2.
wiadomo, że minimum będzie albo na przedziale [t1, t2] (w przypadku gdy zawiera
liczbę całkowitą), albo poza tym przedziałem, ale jak najbliżej niego, tzn.
minimum wynosi floor(t1) lub ceil(t2) (podłoga i sufit).