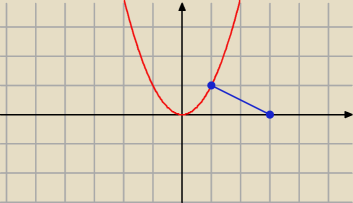
analiza matematyczna anastazja : oblicz odległość punktu (3,0) od wykresu funkcji y= x²

Jerzy: A = (3,0) B = (x,x²) |AB| = d = √(x² − 0)² +(x − 3)² i d ≥ 0 d² = x⁴ + (x − 3)² i szukasz minimum tej funkcji i wynik pierwiastkujesz.

PW: Na wykresie mamy punkty (x, x²), kwadrat odległości dowolnego z nich od punktu (3, 0) jest równy (x−3)² + (x² − 0)² czyli d(x) = x⁴ + x² − 6x + 9 − trzeba znaleźć punkt x₀, w którym d osiąga minimum i obliczyć √d(x₀).

anastazja: w jaki sposób szuka się minimum funkcji, kiedy nie mamy przedziału?

Jerzy: Szukasz minimum lokalnego.

anastazja: czyli liczę pochodną, póżniej z tego miejsca zerowe i szukam min?

Jerzy: Dokładnie tak.Pochodna musi się zerować i zmieniać znak z ujemnego na dodatni, bo wtedy funkcja osiaga minimum lokalne.

anastazja: pochodna 4x³+2x−6 pierwiastki x1=3/2 x2=−1 d(3/2)= 7 5/16 minimum lokalne co dalej mam wykonać?

PW: anastazjo, jak to "nie mamy przedziału"? Funkcja jest określona dla dowolnej liczby x (dla dowolnej x istbieje punkt (x, x²) na paraboli).

anastazja: mogłabym prosić o sprawdzenie wyniku?

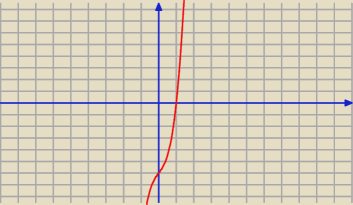
PW: d'(x) = 4x³ + 2x − 6 − dobrze. Miejsce zerowe d' to liczba 1: d'(1) = 4(1)² + 2(1) − 6 = 0. Innego miejsca zerowego nie ma (to by trzeba uzasadnić, ja posłużę się z lenistwa wykresem d'(x).

PW: Oj, anastazjo, podejrzewam że dla dunkcji trzeciego stopnia policzyłaś deltę w celu znalezienia miejsc zerowyxh

anastazja: liczyłam z hornera, dziękuję za poprawienie, teraz minimum lokalne wynosi 5, jak mam dojść do wyniku?

anastazja: wynik to √5?

janek191:

anastazja: dziękuję

jc: d' jest funkcją rosnącą bo to suma dwóch funkcji rosnących. Dlatego ma co najwyżej jedno miejsce zerowe.