funkcja liniowa
Jolanta: Prosiłabym o podanie wzoru funkcji liniowej,której wykres nachylony jest do OX pod kątem α i
| | −60 | |
przechodzi przez punkt A(12,−6) jeśli cosα= |
| |
| | 61 | |
25 lis 23:33
Blee:
| | −60 | | √612 − 602 | | √1*121 | | 11 | |
cos α = |
| −> sinα = |
| = |
| = |
| |
| | 61 | | 61 | | 61 | | 61 | |
podstawiasz punkt A i wyznaczasz współczynnik 'b'
25 lis 23:39
Jolanta: | | −11 | |
To zrobiłam ale zastanawiałam się,czy tgαnie może być |
| |
| | 60 | |
25 lis 23:42
25 lis 23:42
Blee:
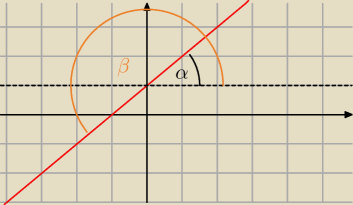
mogłoby być jedynie w przypadku w którym sin (kąta nachylenia) < 0 ... a co za tym idzie ...
kąt były w III ćwiartce ... a co za tym idzie ... były to kąt
β, a nie kąt
α.
Kąt nachylenia prostej bierzemy z przedziału <0
o;180
o) (czyli nie ma kąta nachylenia 180
o
... jest tylko 0
o)
25 lis 23:46
Blee:
co innego gdyby to były wektory (i byśmy patrzyli na zwroty tychże wektorów).
W przypadku nachylenia dwóch prostych (czyli w tym także prostej do prostej OX) wybieramy
zawsze mniejszy z tychże 'możliwych' kątów.
25 lis 23:47
a7: mi wychodzi to samo, tangens może być ujemny
25 lis 23:47
Jolanta: | | 121 | |
Z jedynki trygonometrycznej sin2α= |
| |
| | 3721 | |
25 lis 23:50
a7: ja korzystałam z wzoru 1/cosα − cosα=sinα*tgα
25 lis 23:51
Blee:
Jolanta −−− przeczytaj co napisałem i zrozum ... informacja: cosα < 0 jest równoznaczna z
tym, że ... tgα < 0 i co za tym idzie ... funkcja jest malejąca
25 lis 23:53
Blee:
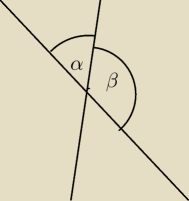
albo jak wolisz.
Który z tych kątów jest kątem nachylenia do siebie tych dwóch prostych

α czy β

25 lis 23:54
Jolanta: | | 12 | |
Nie widziałam tego wpisu ,gdy pisałam. A jezeli sinα= |
| A=(−1−4) sa dwa wzory prostych |
| | 13 | |
?
25 lis 23:59
Jolanta: Blee dziekuję za pomoc

26 lis 00:03
a7: jeżeli sin α=12/13 to tgα=−12/5
y=−12/5 *x +b
y=−125x−625
26 lis 00:09
a7: ?
26 lis 00:09
26 lis 00:12
Jolanta: | | 25 | | 5 | | −5 | |
sinα>0 1 i 2 ćw cosα=√ |
| cosα= |
| cosα= |
| |
| | 169 | | 13 | | 13 | |
26 lis 00:14
sobek:
Równanie prostej: y = a(x − x0) + y0, w tym przypadku y = a(x − 12) − 6, a = tgα
26 lis 00:14
a7: sinα jest 12/13 i A jest w IV cwiartce więc α musi chyba być z drugiej cwiartki skoro jest
dodatni i żeby prosta przechodziła przez punkt A w IV−tej ćwiartce
cos jest więc ujemny, jest więc "tylko" jeden tagens równy −12/5
26 lis 00:15
26 lis 00:21
a7:
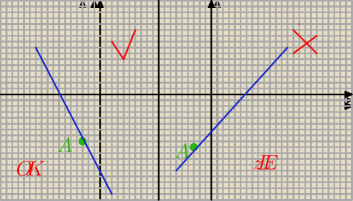
26 lis 00:21
a7: 
26 lis 00:22
Jolanta: Zgodnie z tym co napisał Blee kąt nachylenia <1800
obydwa równania to spełniają
26 lis 00:25
a7: no to nie wiem, może rzeczywiście obydwa, może jeszcze Blee się odezwie
26 lis 00:31
Blee:
a7 −−− a niby co ma ćwiartka w której jest punkt A do kąta nachylenia prostej przechodzącej
przez tenże punkt?
Moim zdaniem, jeżeli sinα jest podany to są dwie możliwe proste i podanie tylko jednej z nich
uważałbym za błąd.
26 lis 00:32
a7: już rozumiem, ok, dzięki
26 lis 00:34
 mogłoby być jedynie w przypadku w którym sin (kąta nachylenia) < 0 ... a co za tym idzie ...
kąt były w III ćwiartce ... a co za tym idzie ... były to kąt β, a nie kąt α.
Kąt nachylenia prostej bierzemy z przedziału <0o;180o) (czyli nie ma kąta nachylenia 180o
... jest tylko 0o)
mogłoby być jedynie w przypadku w którym sin (kąta nachylenia) < 0 ... a co za tym idzie ...
kąt były w III ćwiartce ... a co za tym idzie ... były to kąt β, a nie kąt α.
Kąt nachylenia prostej bierzemy z przedziału <0o;180o) (czyli nie ma kąta nachylenia 180o
... jest tylko 0o)
 albo jak wolisz.
Który z tych kątów jest kątem nachylenia do siebie tych dwóch prostych
albo jak wolisz.
Który z tych kątów jest kątem nachylenia do siebie tych dwóch prostych  α czy β
α czy β 


