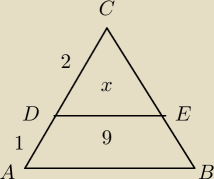
 W trójkącie ABC poprowadzono odcinek DE równoległy do AB.
Wiadomo, że |CD|=2, |AD|=1, pole trójkąta DEC to x, zaś pole trapezu ABED to 9. Zatem prawdziwa
jest równość:
A. 9x= 54
B. 9x= 12
C. 9x=1
D. 9x= 13
W trójkącie ABC poprowadzono odcinek DE równoległy do AB.
Wiadomo, że |CD|=2, |AD|=1, pole trójkąta DEC to x, zaś pole trapezu ABED to 9. Zatem prawdziwa
jest równość:
A. 9x= 54
B. 9x= 12
C. 9x=1
D. 9x= 13
| PCDE | 4 | x | |||
= | a wiemy że to jest = | ||||
| PABC | 9 | x+9 |
| x | 4 | 9 | 5 | ||||
= | ⇔ 9x = 4x + 4*9 ⇔ 5x = 4*9 ⇔ | = | |||||
| x+9 | 9 | x | 4 |
| 9+x | 3 | ||
=( | )2 | ||
| x | 2 |
| 9 | 9 | ||
+1= | |||
| x | 4 |
| 9 | 5 | ||
= | |||
| x | 4 |