W trójkącie równoramiennym 𝐴𝐵𝐶 (𝐴𝐵 = 𝐴𝐶) ∢𝐴 = 20°. 𝐷 i 𝐸 są takimi pu
XDD: W trójkącie równoramiennym 𝐴𝐵𝐶 (𝐴𝐵 = 𝐴𝐶) ∢𝐴 = 20°. 𝐷 i 𝐸 są takimi punktami
odpowiednio na bokach 𝐴𝐵 i 𝐴𝐶, że ∢𝐷𝐶𝐵 = 50°, a ∢𝐸𝐵𝐶 = 60°. Wyznacz miarę kąta
𝐷𝐸𝐵.
Mila:
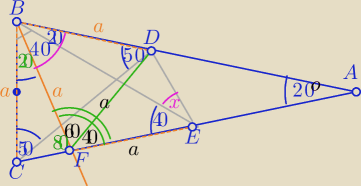
|∡B|=|∡A|=(180−20):2=80
1) Odpowiednio zaznaczam miary kątów, obliczone z sumy kątów w trójkątach
ΔCBD− Δrównoramienny⇔|BC|=|BD|=a
2) Rysuję pomocniczą półprostą BF ,taką, że :
|∡CBF|=20
o − otrzymuję równoramienny ΔCFB
3) łączę punkty F i D otrzymuję równoramienny ΔFBD o kącie ostrym między ramionami60
o⇔
że Δ FBD jest trójkątem równobocznym
4) uzupełniam miary katów na rysunku ⇒
ΔBEF− Δrównoramienny
|FE|=a⇔
ΔDEF jest trójkątem równoramiennym o kącie 40
o między ramionami
x+40
o=(180−40):2
x+40 =70
o
x=30
o
==========
 |∡B|=|∡A|=(180−20):2=80
1) Odpowiednio zaznaczam miary kątów, obliczone z sumy kątów w trójkątach
ΔCBD− Δrównoramienny⇔|BC|=|BD|=a
2) Rysuję pomocniczą półprostą BF ,taką, że :
|∡CBF|=20o − otrzymuję równoramienny ΔCFB
3) łączę punkty F i D otrzymuję równoramienny ΔFBD o kącie ostrym między ramionami60o⇔
że Δ FBD jest trójkątem równobocznym
4) uzupełniam miary katów na rysunku ⇒
ΔBEF− Δrównoramienny
|FE|=a⇔
ΔDEF jest trójkątem równoramiennym o kącie 40 o między ramionami
x+40o=(180−40):2
x+40 =70o
x=30o
==========
|∡B|=|∡A|=(180−20):2=80
1) Odpowiednio zaznaczam miary kątów, obliczone z sumy kątów w trójkątach
ΔCBD− Δrównoramienny⇔|BC|=|BD|=a
2) Rysuję pomocniczą półprostą BF ,taką, że :
|∡CBF|=20o − otrzymuję równoramienny ΔCFB
3) łączę punkty F i D otrzymuję równoramienny ΔFBD o kącie ostrym między ramionami60o⇔
że Δ FBD jest trójkątem równobocznym
4) uzupełniam miary katów na rysunku ⇒
ΔBEF− Δrównoramienny
|FE|=a⇔
ΔDEF jest trójkątem równoramiennym o kącie 40 o między ramionami
x+40o=(180−40):2
x+40 =70o
x=30o
==========