Stosując postać wykładniczą rozwiąż Adrian: Stosując postać wykładniczą rozwiąż: a) |Z⁸| = Z⁴ Obliczyłem, że dla: k = 0 φ = 0 k = −1 φ = ^π₂ k = −2 φ = π k = −3 φ = ³₂π Wyniki wyszły mi takie jak na zajęciach, jednak tu powstaje problem, ponieważ nie wiem jak mam obliczyć pierwiastki Z₀ = 0 Z₁ = 1*e⁰ⁱ=1 Z₂ = i Z₃ = −1 Z₄ = −i

Adamm: nie rozumiem. Z czym problem?

Adrian: Obliczyłem kilka kątów φ i teraz muszę zaznaczyć te rozwiązania na osi i aby to zrobić, trzeba obliczyć te pierwiastki Z₀ itd. i tutaj właśnie nie wiem jak to zrobić, aby takie wyniki otrzymać

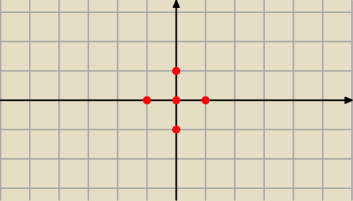
Adamm: narysować jest bardzo prosto

PW: A policzyć "trygonometryczni" jak chciałeś, trochę gadatliwie, np.: |z⁸| = |z|⁸ z= |z|e^iφ, a więc z⁴ = |z|⁴e^4iφ, równanie ma postać |z|⁸ = |z|⁴e^4iφ, skąd |z| = 0 lub (1) |z|⁴ = e^4iφ. Lewa strona jest liczbą rzeczywistą dodatnią, zatem e^4iφ = cos(4φ) + isin(4φ) oznacza, że sin((4φ) = 0 i cos((4φ) > 0 4φ = 0 lub 4φ = 2π lub 4φ = 4π lub 4φ = 6π

	π		3π
φ = 0 lub φ =		lub φ =π lub φ =		,
	2		2

a ponieważ równość (1) oznacza również, że |z|⁴ = 1,

	π		π
z1 = e0, z2 = eπi/2 = cos		+isin		= i, z3 = cosπ +isinπ = −1,
	2		2

	3π		3π
z4 = = cos		+isin		= − i.
	2		2

Adrian: Bardzo dziękuję Wam za pomoc, wirtualne piwko dla was

Mila: |z⁸|=r⁸*e^i*0 z⁴=r⁴*e^4α*i r⁴*e^4α*i=r⁸*e^i*0 r=0 to z=0 lub r>0 ⇔r=1 Mamy równanie : 1*e^4α*i=1*e^i*0

	2kπ
4α=0+2kπ, k∊{0,1,2,3}⇔α=
	4

z₀=1*(cos0+i sin0)=1

	π		π
z1=cos(		+i sin		)=i
	2		2

z₂=cosπ+isinπ=−1

	3π		3π
z3=cos(		+i sin		)=−i
	2		2

=========================

PW: Mila, ja też to robię, żeby nie wyjść z wprawy. A przyznam się, że idzie mi coraz ciężej

Mila: Eee! , zmyślasz i szybszy byłeś ode mnie Pozdrawiam.

daras: to teraz na wyścigi robicie?

Mila: Nikt się nie ściga, podczas pisania nie widać, że ktoś inny rozwiązuje. Zażartowałam z tą szybkością. Jeśli Cię razi mój wpis , to mogę usunąć moje rozwiązanie

PW: E tam, po prostu przyjaźnie zagaduję. Nie robimy żadnych wyścigów.Odpowiedź wymaga nieraz (u mnie przynajmniej) kilkunastu minut, a nawet więcej, i w tym czasie inni już są szybsi. Ja cieszę się, gdy inny użytkownik rozwiązał podobnie albo lepiej.

Mila: