Oblicz monotoniczność i ekstremum funkcji Grzesiu Baraniak:

x3
x−1

Czy przedział monotoniczność to FX>0→xe(³₂, +∞) a FX<0 xe(−∞,0)u(0,³₂) i ma fmin w punkcie ³₂?

janek191:

Grzesiu Baraniak: Nic z tego nie rozumiem

janek191:

	3 x2*( x −1) − x3		2 x3 −3 x2
f '(x) =		=
	( x −1)2		( x −1)2

więc f '(x) < 0 ⇔ 2 x³ − 3 x² < 0 ⇔ x²*( 2 x − 3) < 0 ⇔ x <1,5 zatem f maleje w ( − ∞, 1), ( 1, ³₂) f rośnie w ( ³₂, +∞) Asymptota pionowa : x = 1

janek191: Minimum lokalne w x = ³₂ równe f( ³₂)

Grzesiu Baraniak: A czemu maleje od −∞ do 1 ? A nie do 0?

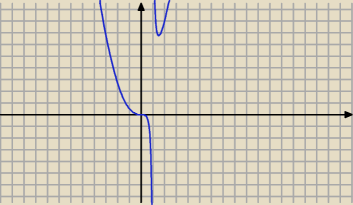
janek191: Funkcja f maleje w przedziale ( − ∞ , 1) ∊ Df oraz w przedziale ( 1, ³₂) ∊ Df Wtedy y przyjmuje wartości od +∞ do − ∞. Funkcja f rośnie w przedziale ( ³₂, +∞) ∊ Df. Wtedy y przyjmuje wartości od f( ³₂) do +∞ dziedzina funkcji Df = ℛ \ { 1} Patrz na wykres funkcji f.

janek191: Jeżeli pochodna f '(x) < 0 to f maleje. Jeżeli f '(x) > 0 to f rośnie.

Grzesiu Baraniak: Ok wszystko rozumiem tylko czemu tam jest przedzial (−∞, 1), przecież x²=0

Jerzy: Ta funkcja ma asymptotę pionową: x = 1 , czyli nie ma wartości dla x = 1 ( nie należy do dziedziny )

Jerzy: I co z tego,że x² = 0 ?

Grzesiu Baraniak: Więc miejsca zerowe z pochodnej 2x³−3X² to x=0 i x=³₂

Jerzy: Tak, ale w punkcie x = 0 pochodna nie zmienia znaku, czyli nie ma ekstremum lokalnego.