Układy równań
Marta: Rozwiąż układ równań..Jakieś sugestie?
x2+y2−2x−6y+9=0
x2+y2+2x−2y−3=0
21 lis 00:11
asd:
Odejmij stronami
odp: (0,3), (1,2)
21 lis 00:39
asd:
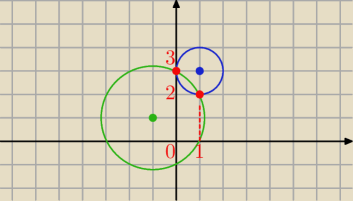
21 lis 00:45
Marta: OK., dziękuję. Wyjdą mi te pierwsze współrzędne, a skąd drugie?
21 lis 00:45
asd:
Po dodaniu stronami otrzymasz:
x+y=3 ⇒ y= 3−x
to x2+(3−x)2−2x−6(3−x)+9=0
................
2x2−2x=0 ⇒ x(x−1)=0 ⇒ x=0 v x= 1 to y=3 v y=2
21 lis 00:49
Marta: Dziękuję bardzo , przemyślę to jeszcze bo coś już nic nie rozumiem

21 lis 00:55
asd:

21 lis 00:56
Marta: Czy to będzie tak:
x2+y2+2x−2y−3=0
x(x+2)+y(y−2)=3
x+y=3, więc y= 3−x i wtedy podstawiam do pierwszego równania, tak to jest zrobione?
21 lis 08:45
janek191:
x2 + y2 −2 x − 6 y + 9 = 0
x2 + y2 + 2 x −2 y −3 = 0
−−−−−−−−−−−−−−−−−−−− odejmujemy stronami
−2 x − 6 y + 9 − 2 x + 2 y + 3 = 0
− 4 x − 4 y = − 12 / : ( − 4)
x + y = 3
y = 3 − x
−−−−−−
Wstawiam 3 − x za y do I równania
x2 + ( 3 − x)2 −2 x − 6*(3 − x) + 9 = 0
x2 + 9 − 6 x + x2 − 2 x − 18 +6 x + 9 = 0
2 x2 −2 x = 0
2 x*( x − 1) = 0
x = 0 lub x = 1
więc
y = 3 − 0 = 3 lub y = 3 − 1 = 2
Odp.
A = ( 0, 3) B = ( 1, 2)
======================
21 lis 09:16
Marta: Ojej źle coś kumam. Dziękuję bardzo. A to zrobiłam dobrze?
x2+y2=25
xy=12
x2+y2=25
xy=12/:x , więc y=12x
x2+(12x)2=25
x4+144=25 x2
x4−25x2+144=0
t=x2
t2−25t+144=0
t1=4, t2=3, napisałam w skrócie, czy tak wyjdzie?
21 lis 09:28
PW: To supertrudne zadanie mogłaś rozwiązać w pamięci:
xy = 12 − najprostsze rozwiązanie to x = 3 i y = 4 lub odwrotnie:x=4 i y = 3.
Tak się składa, że
32 + 42 = 25,
a więc rozwiazania już mamy.
Jedyna wątpliwość: czy nie ma więcej rozwiązań − jak myślisz?
21 lis 11:51
Marta: Nie ma , bo gdyby x=2, y=6 to x
2+y
2 nie równałoby się 25, podobnie z x=1 i y=12
Dziękuję serdecznie, mimo drobnej ironii

21 lis 12:33
PW: To nie była ironia. Chciałem zwrócić uwagę, że zgadywanie rozwiązań jest równie dobrym (a
czasami nawet lepszym) sposobem.
Twoje uzasadnienie byłoby dobre, gdyby w treści zadania podano, że rozwiązania mają być parami
liczb naturalnych, ale takiego założenia w treści zadania nie ma.i
| | 12 | |
Poprawne uzasadnienie: okrąg x2+y2 = 52 − hiperbola y = |
| mają 4 punkty wspólne. |
| | x | |
(rozwiązaniami są jeszcze pary (−3, −4) i (−4, −3)

21 lis 12:49
piotr: t2−25t+144=0
Δ=7
t1 = 9 ∨ t2 = 16
⇒
x2 − 9 = 0 ∨ x2 − 16 = 0
itd.
21 lis 13:24
Marta: Dziękuję

21 lis 13:37
Mila:
Możesz tak liczyć:
x
2+y
2=25
xy=12
======
(x+y)
2−2xy=25
(x+y)
2−2*12=25
(x+y)
2=49
x+y=7 lub x+y=−7
y=7−x lub y=−7−x
==================== Podstawienie do drugiego równania
x*(7−x)=12 lub x*(−7−x)=12
1) −x
2+7x−12=0
x=3 to y=4 lub x=4 to y=4
(3,4) (4,3)
lub
−x
2−7x−12=0⇔x
2+7x+12=0
x
x=−4 to y=−3
lub x=−3 to y=−4
(−4,−3), (−3,−4)
Dłuuuuugi sposób, ale bez równania dwukwadratowego

Wybieraj najlepsze wg Ciebie rozwiązanie

21 lis 15:10
PW:
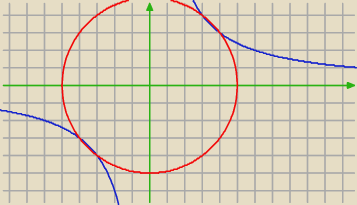
Ilustracja pokazuje okrąg i hiperbolę − cztery punkty wspólne.
21 lis 16:19






 Wybieraj najlepsze wg Ciebie rozwiązanie
Wybieraj najlepsze wg Ciebie rozwiązanie
 Ilustracja pokazuje okrąg i hiperbolę − cztery punkty wspólne.
Ilustracja pokazuje okrąg i hiperbolę − cztery punkty wspólne.