Moduł - liczba rozwiązan Patryk: Witam, mam takie zadanie: Określ liczbę rozwiązań równania w zależności od parametru a. √2|x| − x² = a Podniosłem do kwadratu po tym jak określiłem dziedzine: x ∊<−2; 2> i a≥0. Wychodzi mi 2|x| − x² = a² I dalej z określeniem rozwiązań nie miałem problemu, ale tak myślę w jaki sposób wpływa a² na rozwiązania. Bo zbiór wartości mam okreslony w: <0; 1>. Ale co by było gdyby miał np.<0; 5> ? Skoro były by wartości większe od 1 to wtedy np. zamiast a=5 napisałbym a = 25?

Blee: Proszę −−− wyjaśnij swoje pytanie

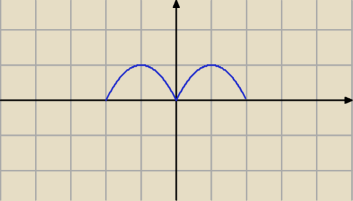
Godzio: Niech f(x) = − x² + 2x. Przekształćmy funkcję nakładając wartość bezwzględną na argument: f(|x|) = − |x|² + 2|x| = − x² + 2|x| Wykonujemy rysunek i odczytujemy: Gdy a² < 1 równanie ma 4 rozwiązania Gdy a² = 1 równanie ma 2 rozwiązania Gdy a² > 1 lub a < 0 równanie nie ma rozwiązań.

Patryk: A co by było gdybym miał inne wartości niż te z <0;1>? (Przykład): Powiedzmy, że dla wartości większych od 7 mam dwa rozwiązania, obojętnie zresztą ile rozwiązań, mi chodzi o sam zapis, to wtedy zapisać mam a>√7 czy a²>7?

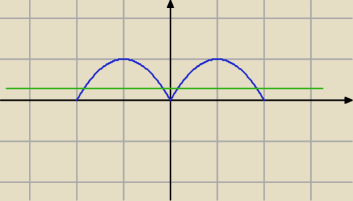
Godzio: Zakładając, że wierzchołek byłby w 7, a nie w 1 (jak teraz) musielibyśmy rozwiązać nierówność a² < 7 itd. Pamiętaj, że po obu stronach równania masz dwie funkcje: f(x) = − x² + 2|x| oraz g(x) = a² Druga funkcja w żaden sposób nie zależy od x, stąd wniosek, że jest stała. Mamy więc wykres funkcji f(x) oraz wykres funkcji g(x), która jest prostą poziomą. W zależności od ilości punktów przecięcia się wykresów f(x) i g(x) mamy liczbę rozwiązań.

	1		1		1
Na wykresie przykład: a2 =		⇒ a ∊ {−		,		}
	4		2		2

	1
Dla takich 'a' otrzymujemy funkcję g(x) =		i jak widać mamy 4 punkty przecięcia, a stąd
	4

4 rozwiązania.

Godzio: Po tych wyjaśnieniach chyba nie odpowiedziałem precyzyjnie − gdybyś miał dla wartości większych od 7 mielibyśmy nierówność a² > 7, a stąd a > √7 lub a < − √7 (pamiętaj, że przy parzystych wykładnikach otrzymujemy rozwiązanie dodatnie i ujemne)

Patryk: Ok, czyli były by dwa przypadki, a co z założeniem, że a ≥ 0? Tak jak z tym zadaniem, które podałem na początku. Bo żeby podnieść po kwadratu musiałem założyć, że a≥0, więc jeśli musiałbym zapisać a² > 7 to czy mogę rozpatrywać przypadek a<−√7 skoro założenie mówi, że a ≥ 0?

Godzio: Tak, wówczas bierzemy część wspólną i wartości ujemne odrzucamy, jednak gdyby nie było w równaniu pierwiastka, a byłoby a², musielibyśmy dorzucić wartości ujemne.

Patryk: Ok, rozumiem już. Dziękuję wielkie za wytłumaczenie