wyznacz Karolina: Wyznacz równania osi symetrii odcinka o końcach A=(1,2) i B=(3,−2)

M:

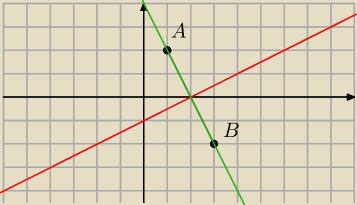
Podstawy Geometrii: A=(1,2) B=(3,−2) Odcinek ma dwie osie symetrii Pierwsza os symetrii to symetralna odcinka (x−x_A)²+(y−y_A)²=(x_B−x)²+(y_B−y)² (x−1)²+(y−2)²=(3−x)²+(−2−y)² x²−2x+1+y²−4y+4=x²−6x+9+y²+4y+4 −4y−4y−2x+6x+5−13=0 −8y+4x−8=0 −8y=−4x+8

	1
y=		x−1 (Czerwona
	2

Druga os symetrii to prosta przechodząca przez punkty A i B

	−2−2
y=		(x−1)+2
	3−1

	−4
y=		(x−1)+2
	2

y=−2(x−1)+2 y= −2x+4 (zielona

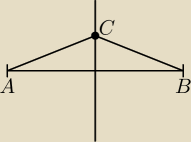Jaś: C = (x, y), A = (1, 2), B = (3, −2)

	1
|AC|2 = |BC|2 ⇒ (x−1)2+(y−2)2=(x−3)2+(y+2)2 ⇒ ... ⇒ y=		x−1
	2