nierówność Szkolniak: proszę o pomoc: (x²+x+1)^x<1 jak się za to zabrać?

Blee: 0) x²+x+1 = 0 Δ = 1 − 4 = −3 < 0 a = 1 −> f(x) = x²+x+1 > 0 dla dowolnego x∊R 1) x > 0 (x²+x+1)^x < 1^x 1.a) x > 1 (x²+x+1)^x < 1^x ⇔ x² + x + 1 < 1 ⇔ x²+x < 0 ⇔ x(x−1) < 0 ⇔ x∊(0,1) → brak rozwiązań 1.b) x < 1 (x²+x+1)^x < 1^x ⇔ x² + x + 1 > 1 ⇔ x²+x > 0 ⇔ x(x−1) > 0 ⇔ x∉<0,1> → brak rozwiązań 2) x < 0

	1		1
(x2+x+1)x =		= {		)|x| < 1|x|
	(x2+x+1)−x		x2+x+1

2.a) x < −1 analogicznie jak wcześniej 1.b) 0 > x > −1 analogicznie jak wcześniej

Szkolniak: w 1.b) nie powinno być przypadkiem x∊(−∞;−1)∪(0;1)?

Blee: x∊(−∞;−1)∪(0;1) ⇔ x∉<0,1> jestem leń i nie chciało mi się dwóch przedziałów pisać

Szkolniak: tylko napisałeś, że jest tam brak rozwiązań, a moim zdaniem rozwiązaniem jest: x∊(−∞;−1)∪(0;1) mylę się?

Blee: po pierwsze w 1.b) masz warunki: x>0 i x<1 a wychodzi przedział x ∊ (−∞;0) u (1;+∞)

Blee: zauważ, że x≥0 masz: x² + x + 1 ≥ 0 + 0 +1 = 1 (dla dowolnego x≥0) ... więc nie ma opcji aby (x²+x+1)^x < 1 gdy x ≥ 0

Godzio: Może trochę inaczej (x² + x + 1)^x < 1 x² + x + 1 > 0 dla x ∊ R ponieważ Δ < 0 Niech x² + x + 1 < 1 ⇒ x² + x < 0 ⇒ x(x + 1) < 0 ⇒ x ∊ (−1,0) Podstawa jest mniejsza od 1, a zatem zmieniamy znak nierówności opuszczając nierówność (x² + x + 1)^x < 1 ⇔ (x² + x + 1)^x < (x² + x + 1)⁰ ⇔ x > 0 −− brak rozwiązań Niech x² + x + 1 > 1 ⇔ x ∊ (−∞,−1) U (0,∞) Podstawa jest większa od 1, zatem nie zmieniamy znaku nierówności: (x² + x + 1)^x < 1 ⇔ (x² + x + 1)^x < (x² + x + 1)⁰ ⇔ x < 0 Stąd otrzymujemy rozwiązanie x ∊ (−∞,−1) Gdy x² + x + 1 = 1 ⇒ x ∊ {−1,0} mamy nierówność fałszywą (1 < 1)

Szkolniak: w 1.b) w momencie rozkładu na czynniki zmieniłeś plus na minus i przez to wychodzi zły przedział zmieniając plus na minus, czy rozwiązaniem wtedy będzie x∊(0;1)?

jc: Nie powinno być po prostu: x<−1 ? x²+x+1 < 1 ⇔ −1 < x < 0 Jeśli −1 < x < 0, to (x²+x+1)^x>1 (wykładnik ujemny) Dla x ≥ 0 x²+x+1 ≥ 0 i (x²+x+1)^x ≥1 (wykładnik dodatni) Dla x < −1, x²+1+1 > 1 i (x²+x+1)^x <1 (wykładnik ujemny). Dla x=−1 mamy 1⁻¹=1.

Szkolniak: zrobione, dzięki wszystkim

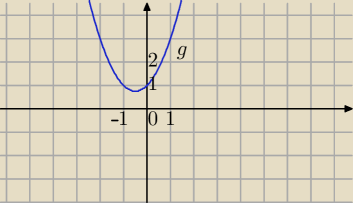
Mila: (x²+x+1)^x<1 f(x)=(x²+x+1)^x g(x)=x²+x+1 x²+x+1>0 dla x∊R 1) g(0)=1 i 1⁰=1 g(−1)=1 i 1⁻¹=1 ⇔ x=0 i x=−1 nie spełniają nierówności 2) g(x)=x²+x+1 g(x)∊(0,1) 0<x²+x+1<1 x∊R i x∊(−1,0) ⇔x∊(0,1) dla g(x)∊(0,1) i x∊(−1,0) wartości f(x) są >1

	−1		3		3
( np, g(		)=		to (		)−1/2=√4/3>1)
	2		4		4

3)g(x)>1⇔ x<−1 lub x>0

	1
(x2+x+1)x<1 dla x<−1 np. g(−2)=3 i 3−2=(		)2<1
	3

Dla x>1 (x²+x+1)^x>1 odp. x<−1