Sprawdzić, czy funkcja jest rożniczkowalna Horqu: Sprawdzić, czy funkcja f(x) = (tg x) / x dla x ∊(−π/2,π/2) 1 dla x=0 jest różniczkowalna w punkcie x0 = 0. Jeśli tak to podać wartość f'(0). Sprawdziłem, licząc granice z dwóch stron do x−>0, że jest ciągła, co zrobić dalej?

Bleee: Liczysz pochodną (z definicji) z punkcie.

Mariusz:

	tg(x+h)   tg(x)   − x+h   x
limh→0
	h

	xtg(x+h)−(x+h)tg(x)   x(x+h)
limh→0
	h

	xtg(x+h)−(x+h)tg(x)
limh→0
	x(x+h)h

	xtg(x+h)−xtg(x)−htg(x)
limh→0
	x(x+h)h

	xtg(x+h)−xtg(x)		tg(x)
limh→0		−limh→0
	x(x+h)h		x(x+h)

	x(tg(x+h)−tg(x))		tg(x)
limh→0		−
	x(x+h)h		x2

	tg(x+h)−tg(x)		tg(x)
limh→0		−
	(x+h)h		x2

	tg(x)+tg(h)   −tg(x) 1−tg(x)tg(h)		tg(x)
limh→0		−
	(x+h)h		x2

	tg(x)+tg(h)−tg(x)+tg2(x)tg(h)   1−tg(x)tg(h)		tg(x)
limh→0		−
	(x+h)h		x2

	tg(h)	1+tg2(x)		tg(x)
limh→0			−
	h	(1−tg(x)tg(h))(x+h)		x2

	sin(h)	1	1+tg2(x)		tg(x)
limh→0				−
	h	cos(h)	(1−tg(x)tg(h))(x+h)		x2

	1+tg2(x)		tg(x)
f'(x)=		−
	x		x2

jc: Zero. Czy Miałeś już Hospitala, czy oczekujesz rachunku bez pochodnych?

Mariusz: Chyba raczej bez pochodnych Tutaj należy sprawdzić czy granice jednostronne są równe

	x+xtg2(x)−tg(x)
limx→0+
	x2

	x(cos2(x)+sin2(x))−sin(x)cos(x)   cos2(x)
limx→0+
	x2

	x−sin(x)cos(x)
limx→0+
	cos2(x)x2

	1		x−sin(x)cos(x)
limx→0+		limx→0+
	cos2(x)		x2

	x−sin(x)cos(x)+sin(x)−sin(x)
limx→0+
	x2

	x−sin(x)		sin(x)		1−cos(x)
limx→0+		+limx→0+		limx→0+
	x2		x		x

	x−sin(x)
limx→0+
	x2

Jeżeli mielibyśmy oszacować tego sinusa to trzeba by było wziąć co najmniej dwa wyrazy jego rozwinięcia w szereg

jc: Mariusz, skąd bierzesz tg²x.

	1		tg x
Mamy policzyć granicę w zerze wyrażenia		(		− 1).
	x		x

	x− sin x
Faktycznie problemem jest granica		.
	x2

Jak pokazać ten fakt, wykorzystując granicę typu (sin x)/x w zerze? Rozwiniecie w szereg czy też Hospital od razu dają zero.

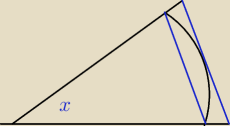
jc: Rysunek jest nieco zniekształcony, aby coś było widać. pole księżyca = (x − sin x)/2 < duży trójkąt − mały trójkąt

	x
0<x − sin x < 2 tg		− sin x =
	2

	x		x		x		x   sin3   2
2(tg		− sin		cos		)=2*
	2		2		2		x   cos   2

	x − sin x
Stąd		→0 przy x→0.
	x2

Mariusz:

	tg(x)
jc a podaj pochodną f(x)=
	x

Blee nie bez powodu sugerował aby policzyć ją z definicji i we wpisie z 21 lis 2019 09:55 ją policzyłem Poza tym dobrze jest zapisywać pochodną tangensa jako (tg(x))' = 1+tg²(x) bo przydaje się to między innymi podczas całkowania

jc: W zadaniu miałeś policzyć pochodną w zerze. Wynik = 0.

	tg u   −1 u
f'(0) = limu→0		= 0
	u

1		tg u		sin u − u cos u
	(		− 1) =
u		u		u2 cos u

	1		1 − cos u		u − sin u
=		(		−		)
	cos u		u		u2

1−cos u		sin2u
	=		→0,
u		u(1+cos u)

drugi wyraz →0