asymptoty ukośne Des:

	2x2 + sin(x)
f(x) =
	x

x ≠ 0

	2x2 + sin(x)		sin(x)
a = limx→ +∞		= 2 +		= 2 + 0 = 2
	x2		x2

	2x2 + sin(x)		2x2 + sin(x) −2x2		sin(x)
b = limx→ +∞		− 2x =		=		= 0
	x		x		x

ukośna: y = 2x Czy można powiedzieć, że jest to asymptota skoro funkcja raz się do niej zbliża, a raz oddala? (tak wynika z wykresu)

ite: Tak, prosta o równaniu y = 2x jest asymptotą tej funkcji.

	sin (x)
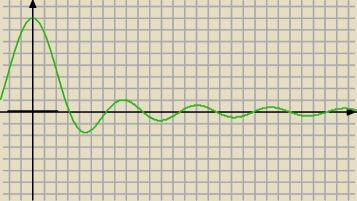
Na rysunku przykład wykresu innej funkcji (f(x)=		), która ma nieskońszenie wiele
	x

punktów wspólnych ze swoją asymptotą.

Des: Dziękuję

daras: @ite jak sięt akie ładne krzywe tutaj maluje?

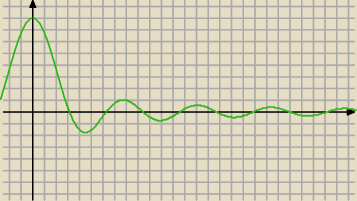Blee: wpisujesz (w tym konkretnym przypadku) 8sin(x)/x i gotowe

daras:

daras: chyba coś nie tak